Assembly Index: A New Way to Measure How Hard Something Is to Make

Series: Assembly Theory | Part: 2 of 9

Walk into any chemistry lab and ask about complexity. You'll get answers about molecular weight, entropy, reaction pathways, thermodynamic favorability. All useful metrics. None of them tell you what Lee Cronin wants to know: How much effort did it take to make this thing?

Not energy. Not time. Not even how many atoms are involved.

How many steps were required to construct it?

This is the assembly index—a radically simple measure of complexity that might be the most important metric in chemistry since Mendeleev organized the periodic table. It doesn't care about your molecule's size, composition, or symmetry. It cares about construction history. How many irreversible operations did the universe have to perform to create this specific arrangement of matter?

A water molecule? Assembly index of 1. You put hydrogen and oxygen together, they bond. Done.

A simple sugar? Maybe 4-6 steps of assembly operations to build that carbon backbone and attach those hydroxyl groups.

A protein? Hundreds. Potentially thousands.

The assembly index measures the minimum number of recursive steps needed to construct an object from elementary building blocks. Not the number of steps that were taken—evolution is messy and wasteful—but the minimum that could be taken if you had perfect knowledge and efficiency.

It's a measure of how much history is compressed into structure.

Why This Matters: The Problem with Shannon Information

Before we dig into the mechanics, understand what the assembly index isn't competing with: it's not trying to replace thermodynamics or information theory. It's measuring something those frameworks miss entirely.

Shannon information measures statistical surprise—how unlikely a particular message is given the distribution of symbols. A random string of letters has high Shannon entropy. A perfectly repeated pattern has low entropy. Both can be complex or simple depending on context.

But Shannon information is ahistorical. It doesn't care how something was constructed, only what pattern resulted. A crystal lattice and a protein might have similar information content by some measures, but wildly different assembly requirements.

The assembly index captures what Shannon doesn't: the trace of causal work required to bring something into existence.

This matters because life doesn't just create patterns. Life creates patterns that couldn't exist without selection pressure operating over time. Random chemistry produces molecules with low assembly indices—they form spontaneously under thermal equilibrium. Life produces molecules with high assembly indices—molecules that require cumulative construction steps that would never occur by chance.

Cronin's claim, and it's a strong one: Assembly index is a biosignature. Show him a molecule with an assembly index above 15, and he'll show you something that required biology—or something biology-adjacent—to make it.

Not because biology is special metaphysically. Because high assembly requires memory and selection, and in this universe, those tend to cluster in systems we call alive.

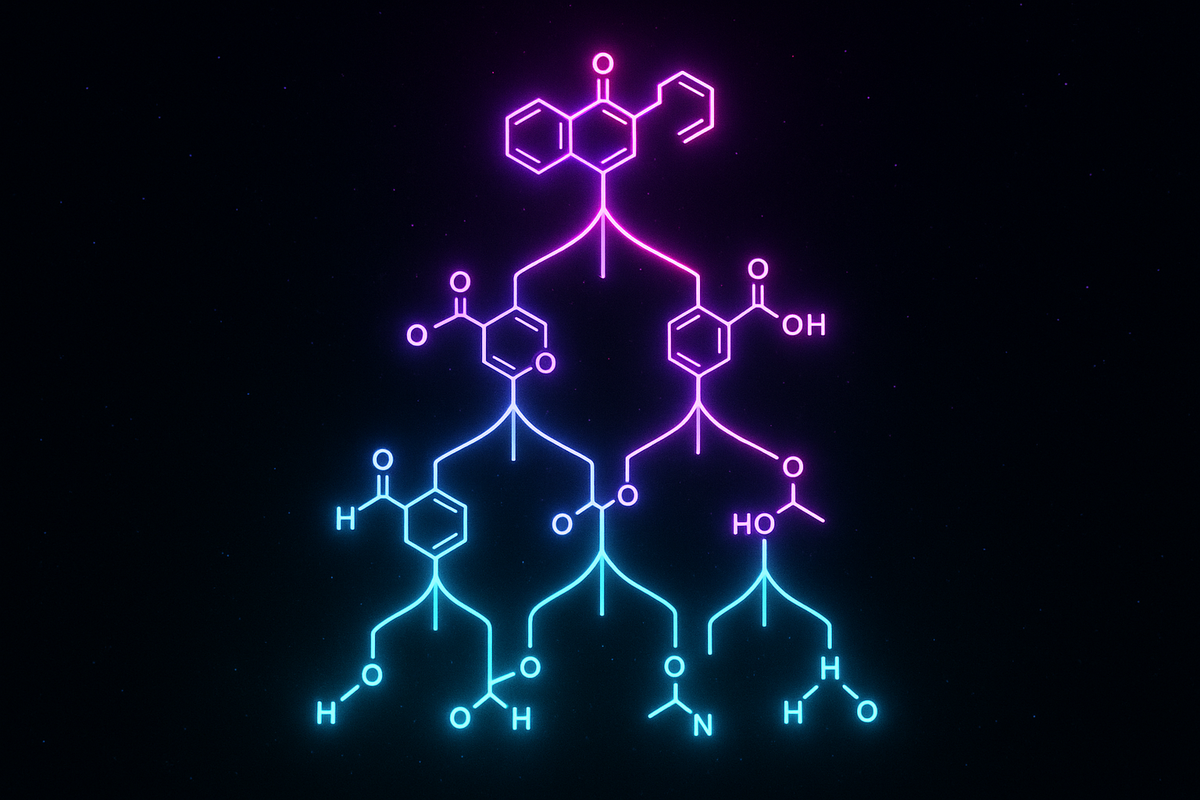
The Mechanics: How to Calculate Assembly Index

Here's where this gets concrete. The assembly index is defined formally, but the intuition is straightforward:

Start with your elementary building blocks. For molecules, that's usually atoms or small functional groups, depending on the scale you choose. For a simple hydrocarbon, your blocks might be CH₂ units. For a complex protein, your blocks might be amino acids.

Count the minimum number of joining operations required to build your target molecule from copies of those blocks, where you can reuse any intermediate structure you've already built.

This is recursion in the mathematical sense. If you've built a subunit, you can use that subunit as a new block for further construction. The assembly index is the depth of this construction tree when optimized for minimum steps.

Example: benzene (C₆H₆).

You could build it atom by atom—six carbon atoms, six hydrogens, figure out the bonding. That's inefficient.

Better: recognize that benzene is a ring of CH units. Build one CH unit (assembly step 1). Join two CH units (step 2). Join three to make half the ring (step 3). Join two halves (step 4). Assembly index: 4.

But benzene forms spontaneously under the right conditions. It's simple chemistry with low assembly demand.

Now try taxol (C₄₇H₅₁NO₁₄)—the cancer drug derived from Pacific yew bark. Taxol has an assembly index around 40-50 depending on your building-block choices. You cannot make taxol by accident. You cannot make it in one step, or five, or ten. It requires cumulative construction through a series of intermediate states that must be stabilized, protected, and sequenced correctly.

The assembly index formalizes this intuition: high assembly molecules encode history.

Assembly as Constraint: Why High-Index Molecules Are Rare

Here's the deeper implication: assembly index measures how constrained the construction pathway was.

Low-index molecules have many pathways to formation. There are countless ways to make water, methane, simple alcohols. Shake the right atoms together with enough energy and you'll get them. They sit at the bottom of thermodynamic wells, easily accessible from many directions.

High-index molecules have narrow pathways. There might be only one sequence of steps—or a very small number of sequences—that successfully constructs the target without hitting dead ends or producing stable-but-wrong intermediates.

This is why random chemistry plateaus at assembly index ~10-12. Beyond that threshold, you need guided construction. You need something—an enzyme, a ribosome, an intelligent chemist—that can hold intermediate states stable, prevent off-pathway reactions, and sequence operations in the right order.

You need, in other words, a constructor.

David Deutsch's Constructor Theory (which we'll connect more explicitly in Article #5) argues that physical laws should be reframed in terms of what transformations are possible versus impossible, and what kinds of systems (constructors) can reliably cause those transformations.

Assembly Theory operationalizes this: high assembly index implies the existence of a constructor. A system capable of performing and sequencing the required operations.

In biology, constructors are enzymes, ribosomes, metabolic pathways—machinery that evolved to reliably build high-assembly molecules. In technology, constructors are us: chemists with flasks and protocols, engineers with fabrication tools.

High assembly is a signature of causal work under selection. It's complexity you can't get for free.

What Makes Assembly Different from Other Complexity Measures

Let's compare assembly index to other attempts at quantifying complexity:

Kolmogorov complexity measures the length of the shortest program that outputs a given string. High Kolmogorov complexity means the pattern is incompressible—truly random. But randomness isn't structure. A random polymer has high Kolmogorov complexity but low assembly index because it requires no specific construction sequence.

Thermodynamic depth (proposed by Seth Lloyd) measures the cumulative thermodynamic cost of all steps required to construct something. This is closer to assembly, but it's harder to calculate and depends on environmental conditions—temperature, pressure, available energy gradients.

Shannon entropy we've discussed—it measures surprise given a distribution, not construction difficulty.

Lempel-Ziv complexity measures how many new patterns emerge as you scan through a sequence. It's useful for data compression but doesn't distinguish between patterns that arise spontaneously and patterns that require directed assembly.

The assembly index sits in a useful middle ground: It's computationally tractable (you can measure it experimentally via mass spectrometry fragmentation patterns, which is Cronin's actual method). It's substrate-independent (works for molecules, but conceptually applicable to other domains). And crucially, it correlates with selection history in a way other measures don't.

A high-assembly molecule is one that couldn't exist without iterated construction under constraint. That makes it a marker of cumulative evolution, whether biological, technological, or otherwise.

The Experimental Proof: Measuring Assembly Via Mass Spectrometry

Theory is elegant. Experiment is decisive.

Cronin's team doesn't calculate assembly indices by hand-counting construction steps. They measure them using tandem mass spectrometry (MS/MS). Here's how:

You ionize your sample molecule, accelerate it through a magnetic field, and smash it into fragments. The fragmentation pattern—which pieces break off, how many different fragment sizes appear—reflects the molecule's internal structure and bonding complexity.

Molecules with high assembly index fragment into many distinct pieces of varying sizes because they have many subunits that were assembled stepwise. Molecules with low assembly index fragment into fewer, more uniform pieces because their structure is simpler and more symmetrical.

Cronin operationalized this: The assembly index correlates with the molecular assembly number (MA), which is the count of unique fragment peaks weighted by their abundance in the mass spectrum.

They tested this across hundreds of molecules:

• Organic molecules synthesized abiotically (low MA, low assembly index)
• Biological molecules extracted from living cells (high MA, high assembly index)
• Complex synthetic molecules made in the lab (high MA, high assembly index)

The threshold consistently appeared around MA = 15. Below that, molecules can form spontaneously. Above that, you need life or life-equivalent chemistry.

No overlap. No ambiguity. Biology doesn't just make different molecules—it makes molecules with quantifiably higher assembly demands.

Assembly and the Arrow of Time: Why Construction History Can't Be Erased

Here's a subtle but crucial point: Assembly index is irreversible.

Once a high-assembly molecule exists, you can't "un-assemble" it back to lower index by breaking bonds. You can destroy it—fragment it back to elementary components—but that doesn't reduce its assembly index. That's a measure of what it took to build it, not what it takes to dismantle it.

This makes assembly index a marker of historical depth. The universe doesn't remember most of its past—entropy smooths over details, equilibrium erases structure. But high-assembly objects are frozen history. They encode the sequence of steps that brought them into being.

In this sense, assembly index is an arrow of time. You can tell, just by looking at a molecule's structure, whether it came from a regime of iterated construction (high index) or spontaneous formation (low index). The molecule carries evidence of its causal past.

This connects to Karl Friston's Free Energy Principle (which we'll bridge explicitly in Article #8): living systems minimize free energy by building models of their environment and acting to confirm those models. High-assembly molecules are material predictions—structures built to persist in specific niches, shaped by selection to fit constraints.

Assembly Theory gives us a way to measure the depth of that history. How many predictive iterations, how many rounds of selection and stabilization, were compressed into this particular arrangement of matter?

Why This Reframes the Origin of Life Question

The traditional origin-of-life question goes like this: How did non-living chemistry become living biology?

That framing assumes a sharp boundary—a moment when molecules crossed from "not alive" to "alive." But assembly theory suggests a different picture:

Life is a threshold of cumulative assembly.

Below assembly index ~15, molecules are abiotic—they can form spontaneously, persist in equilibrium, don't require selection. Chemistry at this level is repetitive, predictable, thermodynamically driven.

Above assembly index ~15, molecules are biotic or proto-biotic—they require iterated construction, memory of previous states, selection for persistence. Chemistry at this level is historical, contingent, shaped by cumulative causation.

There's no magic dividing line. There's a gradient of assembly complexity, and somewhere along that gradient, chemistry started encoding enough history that it could reliably reproduce itself and explore higher-assembly space.

Origin of life becomes origin of high assembly. The question shifts from "when did molecules become alive?" to "when did chemistry develop the capacity for cumulative construction?"

That's a tractable question. You can study it experimentally by looking for conditions that enable assembly index to ratchet upward: autocatalytic cycles, compartmentalization, template-driven polymerization, error correction.

Life isn't a category error. It's a phase transition in construction capacity.

The Limits: What Assembly Index Doesn't Measure

Before we get too enthused, let's be clear about what assembly index doesn't capture.

It doesn't measure function. A high-assembly molecule might be biologically useless. Assembly tells you something required cumulative work to make it—not that it does anything interesting once made.

It doesn't measure efficiency. Evolution is a terrible engineer. Biological molecules often have higher assembly indices than necessary because evolution tinkers rather than designs. A rationally designed synthetic molecule might achieve the same function with lower assembly.

It doesn't scale obviously to non-molecular domains. Cronin talks speculatively about applying assembly concepts to culture, cognition, technology—but those extensions aren't rigorous yet. Assembly works for molecules because we can define elementary building blocks and joining operations clearly. For ideas or institutions, that's much harder.

It doesn't explain how constructors arise. Assembly Theory tells you that high-assembly objects require constructors, but it doesn't tell you how the first constructors emerged or what selection pressures shaped them. That's still an open question.

These are real limitations, not deal-breakers. Assembly index is a measurement tool, not a Theory of Everything. It quantifies one specific, important dimension of complexity—construction depth. That's enough to make it revolutionary.

Connecting to AToM: Assembly as Coherence Under Construction Constraints

Let's bring this home to the framework we're building across Ideasthesia.

In AToM terms, M = C/T—meaning equals coherence over time. Coherence is the degree to which a system's components are mutually predictive, fitting together in ways that reduce free energy and enable persistence.

Assembly index is coherence frozen into structure.

A high-assembly molecule is coherent not in the sense of internal harmony (though many are elegantly structured), but in the sense of historical coherence—its parts fit together in ways that required iterated selection to discover and stabilize. Each assembly step is a constraint satisfaction event: the system found a configuration that was stable enough to serve as a platform for the next step.

Low-assembly molecules lack this historical depth. They form when constraints are loose, when many configurations satisfy the thermodynamic requirements. High-assembly molecules form when constraints are tight, when only very specific sequences succeed.

In geometric terms, high assembly corresponds to navigating a high-curvature region of chemical space. Most pathways lead to dead ends or low-complexity attractors. The successful pathway—the one that reaches high assembly—requires something like active inference: prediction (what intermediate is stable?), action (build that intermediate), error correction (discard failed attempts), cumulative learning (reuse successful subunits).

Assembly Theory doesn't invoke these concepts explicitly, but the mathematics align. High assembly implies the machinery of prediction, selection, memory. It implies systems that aren't just thermodynamically stable, but dynamically coherent over iterated construction cycles.

This is why assembly index matters beyond chemistry. It's a measure of how much causal work history has done to bring something into existence. And wherever you find high assembly—in molecules, ecosystems, technologies, cultures—you find systems operating under the same constraints that produce meaning.

Meaning, remember, is coherence that persists under tension. High-assembly molecules are meaningful structures in a literal sense: they encode information about the selection pressures that shaped them, information that enables their continued existence.

Assembly Theory gives us a metric for that encoding. It tells us how deep the history runs.

What This Means for Detecting Life Elsewhere

One last implication before we close: If assembly index is a biosignature, we can use it to search for life on other worlds.

Traditional biosignatures look for specific molecules—oxygen, methane, phosphine—that might indicate biological processes. But those are Earth-centric. Alien biochemistry might not use oxygen. It might not use carbon.

Assembly index is substrate-independent. It doesn't care what your molecules are made of, only how complex their construction pathway is. Show Cronin a silicon-based polymer with assembly index 30, and he'll tell you something life-like made it, even if it doesn't resemble Earth biology at all.

This is the focus of Article #7, where we explore the cosmic implications in detail. But the core insight is here: High assembly is a universal marker for systems that build, remember, and select. Wherever those processes occur, they leave an assembly signature.

If we point our spectrometers at exoplanet atmospheres or analyze samples from Enceladus or Titan, we're not just looking for familiar molecules. We're looking for molecules that couldn't exist without cumulative construction. We're looking for evidence of history compressed into matter.

That's a much broader search space. And it's grounded in a rigorous, measurable metric that doesn't depend on our assumptions about what life "should" look like.

The Bigger Picture: Construction as Fundamental

Step back and consider what assembly theory does conceptually.

It shifts focus from what things are to how they got here. Not the ontology of objects, but the causal pathways that produced them.

This is a profound move. Most of physics is ahistorical—laws that apply timelessly, symmetries that don't care about past states. Assembly Theory insists that for complex systems, history matters irreducibly. You can't understand a protein by analyzing its atoms. You have to understand the selection pressures, the evolutionary pathway, the cumulative construction that made it possible.

This resonates across domains:

• In neuroscience: the brain's structure encodes its developmental and evolutionary history (connectome as high-assembly network)
• In culture: institutions and technologies are high-assembly artifacts shaped by iterated selection (languages, legal systems, architectural styles)
• In cognition: concepts and skills require cumulative learning, building subunits and recombining them into higher-order structures (assembly index of expertise)

Assembly Theory makes explicit what we often sense intuitively: Complexity you can measure is complexity that took work to build. And the more work it took, the more history is encoded, the more we can infer about the systems that did the building.

That's not just a metric. That's a lens for understanding how novelty emerges in the universe.

This is Part 2 of the Assembly Theory series, exploring Lee Cronin's revolutionary framework for measuring complexity through construction history.

Previous: The Chemist Measuring Complexity: Lee Cronin and the Revolution in Origin-of-Life Science
Next: Why Life Chemistry Is Special: What Assembly Theory Reveals About Biological Molecules

Further Reading

• Cronin, L., & Walker, S. I. (2016). "Beyond Prebiotic Chemistry." Science, 352(6290), 1174-1175.
• Marshall, S. M., et al. (2021). "Identifying Molecules as Biosignatures with Assembly Theory and Mass Spectrometry." Nature Communications, 12, 3033.
• Sharma, A., et al. (2023). "Assembly Theory Explains and Quantifies Selection and Evolution." Nature, 622, 321-328.
• Deutsch, D. (2013). "Constructor Theory." Synthese, 190(18), 4331-4359.
• Lloyd, S. (1988). "Black Holes, Demons and the Loss of Coherence." PhD Thesis, Rockefeller University.