Big O Notation: How Algorithms Scale

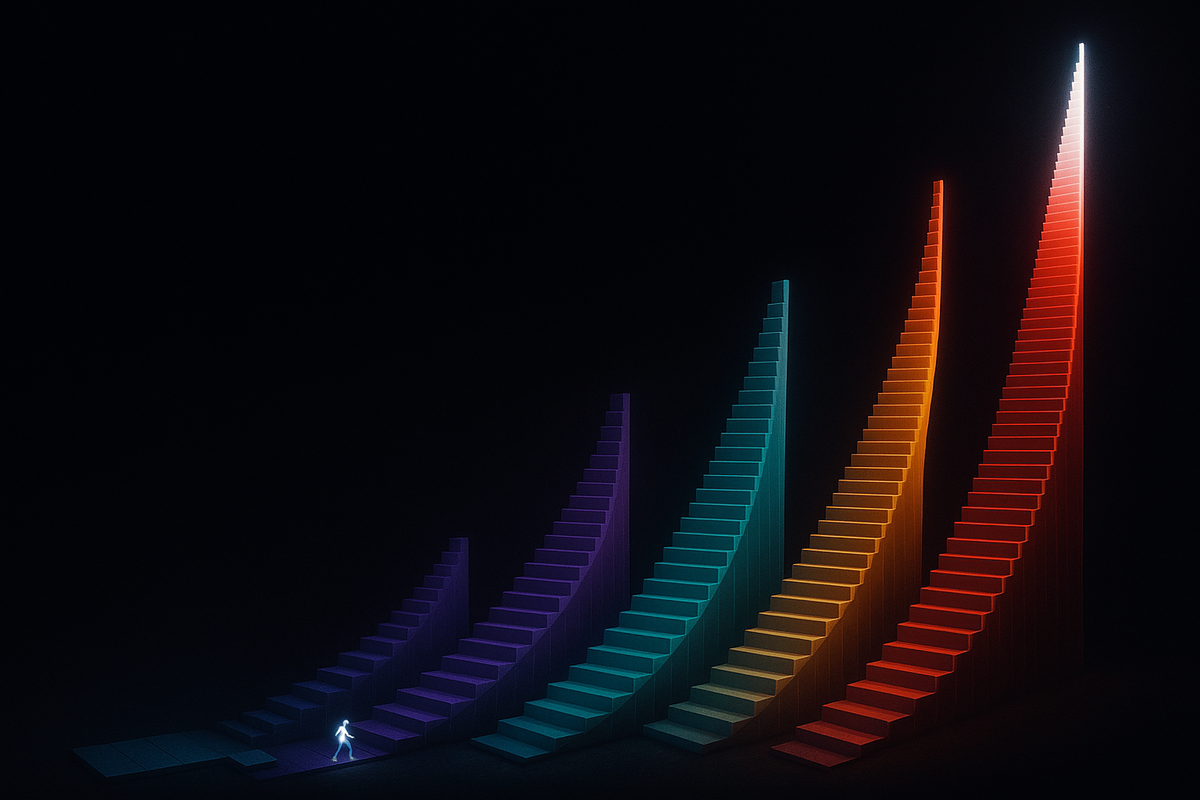
You have 100 items to sort. Your algorithm takes 1 second.

You have 1,000 items. How long does it take?

If your algorithm is O(n): 10 seconds (linear—10× more data, 10× more time).

If it's O(n²): 100 seconds (quadratic—10× data, 100× time).

If it's O(n log n): ~13 seconds (efficient sorting like merge sort).

If it's O(2ⁿ): Doesn't finish before the heat death of the universe.

Big O notation tells you how algorithms scale. Not the exact runtime—the shape of growth as input size increases. And that shape determines whether your code runs in milliseconds or millennia.

The Definition

Big O notation describes the upper bound on the growth rate of an algorithm's time or space complexity as input size n approaches infinity.

Formal: f(n) = O(g(n)) if there exist constants c > 0 and n₀ such that f(n) ≤ c × g(n) for all n ≥ n₀.

Translation: f(n) grows no faster than g(n), ignoring constant factors and lower-order terms.

Intuitive: Big O captures the dominant term as n gets large. It tells you whether your algorithm scales linearly, quadratically, exponentially, or logarithmically.

Common Complexities (From Best to Worst)

O(1) — Constant Time

Runtime doesn't depend on input size.

Examples:

• Array access: arr[5]
• Hash table lookup (average case)
• Simple arithmetic

Why it's powerful: Scalability is perfect. Whether you have 10 items or 10 billion, runtime is the same.

O(log n) — Logarithmic

Halves the problem size each step.

Examples:

• Binary search (sorted array)
• Balanced binary search tree operations
• Heap insertion/deletion

Why it scales: log₂(1,000,000) ≈ 20. Even massive inputs require few operations.

O(n) — Linear

Examines each element once.

Examples:

• Finding max/min in unsorted array
• Summing array elements
• Iterating through a list

Why it's reasonable: Doubling input doubles runtime. Predictable, manageable.

O(n log n) — Linearithmic

Efficient divide-and-conquer.

Examples:

• Merge sort, heap sort, quicksort (average case)
• Fast Fourier Transform (FFT)
• Sorting lower bound (comparison-based sorts can't do better)

Why it's the "good" sorting bound: For n = 1,000,000, n log n ≈ 20 million operations. Feasible on modern hardware.

O(n²) — Quadratic

Nested loops over input.

Examples:

• Bubble sort, insertion sort, selection sort
• Comparing all pairs
• Naive matrix multiplication

Why it struggles: n = 10,000 → 100 million operations. Still manageable. n = 1,000,000 → 1 trillion operations. Starts to hurt.

O(n³) — Cubic

Triple-nested loops.

Examples:

• Standard matrix multiplication (multiply two n×n matrices)
• Floyd-Warshall (all-pairs shortest paths)

Why it's expensive: n = 1,000 → 1 billion operations. Feasible but slow. n = 10,000 → 1 trillion operations. Ouch.

O(2ⁿ) — Exponential

Doubling input size doubles the exponent.

Examples:

• Brute-force subset enumeration (2ⁿ subsets)
• Solving Tower of Hanoi (2ⁿ - 1 moves)
• Naive Fibonacci (recursive without memoization)

Why it's infeasible: n = 20 → 1 million operations. n = 30 → 1 billion. n = 100 → more operations than atoms in the universe.

O(n!) — Factorial

Catastrophic growth.

Examples:

• Brute-force Traveling Salesman (try all permutations)
• Generating all permutations

Why it's impossible: n = 10 → 3.6 million operations. n = 20 → 2.4 quintillion. n = 30 → exceeds computational capacity of all computers ever made.

Why Big O Ignores Constants

Consider two algorithms:

• Algorithm A: 100n operations
• Algorithm B: 2n² operations

For small n, A is slower (100 × 10 = 1,000 vs. 2 × 100 = 200).

But as n grows:

• n = 1,000: A = 100,000 vs. B = 2,000,000
• n = 10,000: A = 1,000,000 vs. B = 200,000,000

Big O focuses on growth rate, not constants. A is O(n), B is O(n²). Eventually, O(n) always beats O(n²), regardless of constants.

Constants matter in practice (100n might be slower than 2n for realistic n), but Big O tells you the asymptotic winner as n → ∞.

Best, Average, Worst Case

Big O typically describes worst-case complexity, but algorithms have three scenarios:

Best Case (Ω notation)

Minimum time/space required.

Example: Quicksort's best case is Ω(n log n) (perfectly balanced partitions).

Average Case (Θ notation)

Expected performance over random inputs.

Example: Quicksort's average case is Θ(n log n).

Worst Case (O notation)

Maximum time/space required.

Example: Quicksort's worst case is O(n²) (already sorted, bad pivot choice).

Why worst-case matters: Guarantees. If you need reliability (real-time systems, safety-critical code), worst-case bounds are essential.

Analyzing Loops

Single Loop

for i in range(n):
    # O(1) operation

Complexity: O(n). Loop runs n times, each iteration is constant.

Nested Loops

for i in range(n):
    for j in range(n):
        # O(1) operation

Complexity: O(n²). Outer loop runs n times, inner loop runs n times each. Total: n × n.

Dependent Nested Loops

for i in range(n):
    for j in range(i):
        # O(1) operation

Complexity: O(n²). Inner loop runs 0, 1, 2, ..., n-1 times. Sum = n(n-1)/2 = O(n²).

Logarithmic Loop

i = 1
while i < n:
    i *= 2
    # O(1) operation

Complexity: O(log n). i doubles each iteration: 1, 2, 4, 8, ..., n. Number of iterations = log₂(n).

Analyzing Recursive Algorithms

Recursive algorithms yield recurrence relations.

Binary Search

def binary_search(arr, target, low, high):
    if low > high:
        return -1
    mid = (low + high) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        return binary_search(arr, target, mid+1, high)
    else:
        return binary_search(arr, target, low, mid-1)

Recurrence: T(n) = T(n/2) + O(1)

Solution: T(n) = O(log n). Each call halves the problem size.

Merge Sort

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)  # O(n)

Recurrence: T(n) = 2T(n/2) + O(n)

Solution: T(n) = O(n log n). Master Theorem Case 2.

Naive Fibonacci

def fib(n):
    if n <= 1:
        return n
    return fib(n-1) + fib(n-2)

Recurrence: T(n) = T(n-1) + T(n-2) + O(1)

Solution: T(n) = O(φⁿ) where φ ≈ 1.618 (golden ratio). Exponential!

Why so bad? Redundant calculations. fib(5) calls fib(4) and fib(3). fib(4) calls fib(3) again. Massive overlap.

Fix: Memoization or dynamic programming → O(n).

Space Complexity

Big O also describes memory usage.

Examples:

• O(1) space: Fixed memory, regardless of input size (e.g., swapping two variables)
• O(n) space: Array or list storing n elements
• O(n²) space: n × n matrix
• O(log n) space: Recursive call stack for binary search

Trade-off: Time vs. space. Sometimes using more memory reduces time (e.g., memoization).

Amortized Analysis

Some operations are expensive occasionally but cheap on average.

Example: Dynamic array (Python list, C++ vector)

• Appending usually takes O(1)
• Occasionally (when full), array resizes: O(n) to copy elements

Amortized cost: O(1) per append over a sequence of n appends.

Why? Resizing happens infrequently (doubling size each time). Total cost over n appends: O(n). Average: O(n)/n = O(1).

Amortized analysis smooths out worst-case spikes over many operations.

Lower Bounds: Provable Limits

Some problems have proven lower bounds—no algorithm can do better.

Sorting (Comparison-Based)

Lower bound: Ω(n log n)

Proof: There are n! possible orderings. Each comparison gives 1 bit of information (yes/no). To distinguish n! possibilities requires log₂(n!) ≈ n log n comparisons.

Implication: Merge sort and heap sort are optimal for comparison-based sorting. You can't beat O(n log n) without additional assumptions (e.g., counting sort for integers uses non-comparison techniques).

Searching Unsorted Array

Lower bound: Ω(n)

Proof: Worst case, target might be the last element checked. You must examine all n elements.

Matrix Multiplication

Current best: O(n^{2.371}) (Coppersmith-Winograd, improved by others)

Trivial lower bound: Ω(n²) (must read all n² inputs)

Open question: Is matrix multiplication possible in O(n²)? Unknown.

Lower bounds separate what's hard from what's impossible.

P vs. NP: The Million-Dollar Question

P: Problems solvable in polynomial time (O(nᵏ) for some constant k).

NP: Problems where solutions can be verified in polynomial time.

P ⊆ NP (if you can solve quickly, you can verify quickly).

The question: Does P = NP? Can every problem whose solution is easy to verify also be solved quickly?

Example: Sudoku

• Verification: O(n²) (check rows, columns, boxes)
• Solving: Unknown if polynomial. Best algorithms are exponential for general case.

Implications if P = NP:

• Most cryptography breaks (RSA, etc. rely on hard problems)
• Optimization becomes easy (traveling salesman, scheduling, etc.)
• Massive scientific and economic impact

Consensus: Most computer scientists believe P ≠ NP (some problems are inherently hard). But it's unproven. This is one of the Millennium Prize Problems worth $1 million.

NP-Complete Problems

NP-complete: The "hardest" problems in NP. If you solve one in polynomial time, you solve all NP problems in polynomial time.

Examples:

• Traveling Salesman Problem (TSP): Find shortest route visiting all cities
• Boolean Satisfiability (SAT): Does a Boolean formula have a satisfying assignment?
• Knapsack: Select items maximizing value without exceeding weight limit
• Graph Coloring: Color graph with minimum colors such that no adjacent nodes share colors
• Hamiltonian Path: Does a graph have a path visiting all nodes once?

Significance: NP-complete problems are ubiquitous. If P ≠ NP, they're provably hard—no efficient algorithm exists.

Practical approach: Approximation algorithms, heuristics, branch-and-bound, or accept exponential time for small inputs.

When Big O Misleads

Big O is asymptotic—it describes behavior as n → ∞. But real-world n is finite.

Example: Insertion sort (O(n²)) vs. merge sort (O(n log n))

For small n (say, < 10), insertion sort is often faster due to lower constants and better cache locality. Many implementations switch to insertion sort for small subarrays.

Example: Strassen's matrix multiplication is O(n^{2.807}) vs. naive O(n³).

For small matrices (n < 100), naive multiplication is faster due to simpler operations and better hardware utilization.

Takeaway: Big O tells you the eventual winner. For practical n, profile and test.

Real-World Applications

Databases: Index structures (B-trees) guarantee O(log n) search. Without indexing, search is O(n). For millions of records, this is the difference between milliseconds and minutes.

Web search: Google indexes trillions of pages. Linear search would take forever. PageRank + inverted indices + clever data structures make search O(log n) or better.

Machine learning: Training neural networks is O(n × m × e) where n = data size, m = model parameters, e = epochs. Complexity drives GPU usage, distributed training.

Graphics: Rendering 3D scenes involves checking n objects against m pixels. Naive O(nm) is too slow. Spatial data structures (octrees, BSP trees) reduce to O(log n) per pixel.

Compilers: Parsing code is O(n) for most modern parsers. Optimization passes may be O(n²) or worse. Complexity determines compile time.

Optimizing Algorithms

From O(n²) to O(n log n)

Problem: Find duplicates in array.

Naive: Compare all pairs. O(n²).

Better: Sort first, then scan for adjacent duplicates. O(n log n).

Best: Use hash set. Insert and check each element. O(n) average case.

From O(2ⁿ) to O(n)

Problem: Compute Fibonacci F(n).

Naive recursion: O(φⁿ). Exponential.

Memoization: Store computed values. O(n) time, O(n) space.

Iterative: Loop from 1 to n. O(n) time, O(1) space.

Matrix exponentiation: O(log n) time. Uses fast exponentiation.

From O(n³) to O(n^{2.371})

Problem: Matrix multiplication.

Naive: Three nested loops. O(n³).

Strassen: Divide-and-conquer with clever tricks. O(n^{2.807}).

Coppersmith-Winograd (improved): O(n^{2.371}). Impractical due to huge constants, but theoretically faster.

Optimization often means finding better algorithms, not just faster hardware.

Why Big O Matters

Big O is the language of scalability.

• Predict performance: Will this code handle 1,000 users? 1 million? 1 billion?
• Compare algorithms: Which is fundamentally faster as n grows?
• Identify bottlenecks: Where does complexity explode?
• Set expectations: Is this problem tractable or inherently hard?

Without Big O, you're flying blind. With it, you can reason about computational feasibility before writing a line of code.

When someone says "this algorithm scales," they're talking about Big O. When a system collapses under load, it's often because an O(n²) or O(2ⁿ) operation hit production scale.

Big O notation is how we know some problems are literally impossible to solve efficiently—and why we keep searching for better algorithms for the ones that aren't.

Further Reading

• Cormen, Thomas H., et al. Introduction to Algorithms. MIT Press, 4th edition, 2022. (Chapter 3: Growth of Functions)
• Sedgewick, Robert, and Kevin Wayne. Algorithms. Addison-Wesley, 4th edition, 2011. (Analysis of algorithms)
• Knuth, Donald E. The Art of Computer Programming (series). Addison-Wesley. (Rigorous algorithm analysis)
• Sipser, Michael. Introduction to the Theory of Computation. Cengage Learning, 3rd edition, 2012. (P vs. NP, complexity theory)

This is Part 9 of the Discrete Mathematics series, exploring the foundational math of computer science, algorithms, and computational thinking. Next: "Boolean Algebra Explained — The Two-Number System That Built Every Computer."

Part 9 of the Discrete Mathematics series.

Previous: Recurrence Relations: Sequences Defined Recursively Next: Boolean Algebra: The Mathematics of True and False