Change of Base Formula: Converting Between Logarithms

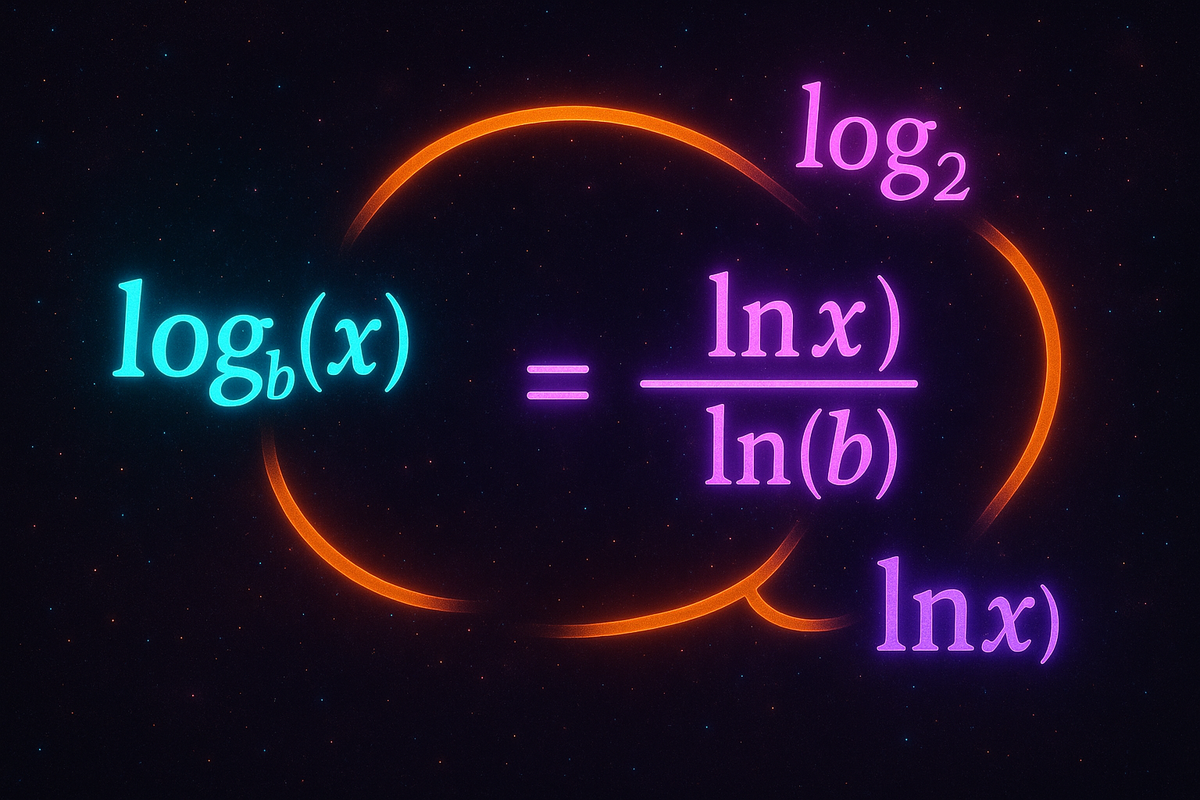
Any logarithm can be computed using any other logarithm.

Your calculator has buttons for log (base 10) and ln (base e). But what if you need log₂(7) or log₅(100)?

Use the change of base formula. It converts any logarithm into a ratio of logarithms you can compute.

log_b(x) = ln(x) / ln(b) = log(x) / log(b)

That's it. Divide two logarithms you can calculate, and you get the logarithm in any base you want.

The Formula

log_b(x) = log_c(x) / log_c(b)

where c can be any base (usually 10 or e).

In practical terms:

log_b(x) = log(x) / log(b) using base 10

log_b(x) = ln(x) / ln(b) using natural log

Both give the same answer. Use whichever your calculator has.

Why It Works

Let log_b(x) = y. This means bʸ = x.

Take log_c of both sides: log_c(bʸ) = log_c(x) y × log_c(b) = log_c(x) y = log_c(x) / log_c(b)

Therefore: log_b(x) = log_c(x) / log_c(b). ∎

The formula works because logarithms are exponents, and the power rule (log of a power is power times log) lets us extract the exponent.

Examples

Example 1: log₂(10)

log₂(10) = log(10) / log(2) = 1 / 0.301 ≈ 3.32

Check: 2^3.32 ≈ 10 ✓

This tells you 10 is about 3.32 doublings above 1.

Example 2: log₃(81)

log₃(81) = log(81) / log(3) = 1.908 / 0.477 = 4

Check: 3⁴ = 81 ✓

When the answer is exact, the division comes out clean.

Example 3: log₅(7)

log₅(7) = ln(7) / ln(5) = 1.946 / 1.609 ≈ 1.209

Check: 5^1.209 ≈ 7 ✓

Example 4: log₇(100)

log₇(100) = log(100) / log(7) = 2 / 0.845 ≈ 2.37

This tells you 100 is about 2.37 powers of 7 above 1.

Common Conversions

Between base 10 and base e:

ln(x) = 2.303 × log(x)

log(x) = 0.434 × ln(x)

The conversion factor is ln(10) ≈ 2.303 (or its reciprocal 0.434).

Between base 2 and base e:

log₂(x) = 1.443 × ln(x)

ln(x) = 0.693 × log₂(x)

The conversion factor is ln(2) ≈ 0.693 (or its reciprocal 1.443).

Between base 2 and base 10:

log₂(x) = 3.322 × log(x)

log(x) = 0.301 × log₂(x)

Solving Equations with Change of Base

Example: Solve 5ˣ = 17.

Take log of both sides: x × log(5) = log(17) x = log(17) / log(5) = 1.230 / 0.699 ≈ 1.76

This is the same as x = log₅(17) ≈ 1.76.

Example: Solve 3^(2x-1) = 7^x.

Take ln of both sides: (2x - 1)ln(3) = x × ln(7) 2x × ln(3) - ln(3) = x × ln(7) x(2 ln(3) - ln(7)) = ln(3) x = ln(3) / (2 ln(3) - ln(7)) x = 1.099 / (2.197 - 1.946) = 1.099 / 0.251 ≈ 4.38

The Ratio Interpretation

log_b(x) / log_b(y) = log_y(x)

The ratio of two logarithms (same base) gives a logarithm in a new base.

Example: log(1000) / log(10) = 3 / 1 = 3 = log₁₀(1000) ✓

Example: ln(8) / ln(2) = 2.079 / 0.693 = 3 = log₂(8) ✓

This is the change of base formula in another form.

Why Different Bases Exist

Base 10 — Human counting, orders of magnitude

• log₁₀(1000) = 3 means "three orders of magnitude"

Base e — Calculus, continuous processes

• ln(x) = ∫₁ˣ (1/t)dt, the natural antiderivative

Base 2 — Computing, information theory

• log₂(x) counts bits, doublings, binary digits

Arbitrary bases — Context-dependent

• log₁₂(x) might matter for time (hours)
• log₆₀(x) might matter for time (minutes)

The change of base formula means you never need a special calculator. Any logarithm is a ratio of logs you already have.

Special Cases

log_b(b) = 1 for any base

log_b(b) = log(b) / log(b) = 1 ✓

log_b(1) = 0 for any base

log_b(1) = log(1) / log(b) = 0 / log(b) = 0 ✓

log_b(bⁿ) = n for any base

log_b(bⁿ) = log(bⁿ) / log(b) = n × log(b) / log(b) = n ✓

The formulas check out.

The Reciprocal Relationship

log_a(b) × log_b(a) = 1

Proof: log_a(b) = log(b) / log(a) log_b(a) = log(a) / log(b)

Multiply: [log(b)/log(a)] × [log(a)/log(b)] = 1 ✓

In other words: log_a(b) = 1 / log_b(a)

If log₂(8) = 3, then log₈(2) = 1/3.

Check: 8^(1/3) = 2 ✓

Mental Estimation

For quick estimates, remember:

• log₂(10) ≈ 3.32 (10 is about 3.3 doublings)
• log₁₀(2) ≈ 0.301 (doubling adds about 0.3 to the log)
• ln(10) ≈ 2.30
• ln(2) ≈ 0.69

Example: Estimate log₃(50).

log₃(50) = log(50) / log(3) ≈ 1.7 / 0.48 ≈ 3.5

Check: 3^3.5 ≈ 47 ✓ (close to 50)

Why This Matters

The change of base formula is liberating. It says:

1. You only need one logarithm. Any base converts to any other.
2. Calculators are enough. You have log and ln; that covers everything.
3. Logarithms are fundamentally the same. They differ by constant factors, not in kind.
4. Solving exponential equations is always possible. Any base, any equation—take a log and divide.

The formula log_b(x) = ln(x)/ln(b) is the universal adapter. It connects all logarithms into one unified framework.

Part 5 of the Logarithms series.

Previous: Natural Logarithm: Why ln Uses Base e Next: Logarithmic Scales: When Numbers Span Many Orders of Magnitude