Complex Numbers Explained

In the 16th century, Italian mathematicians were having public math duels. Solve this equation faster than your opponent, win the prize. Lose, and your reputation is destroyed.
Gerolamo Cardano discovered a formula for solving cubic equations. But there was a problem: sometimes his formula required taking the square root of a negative number. This should be impossible. Negative numbers don't have square roots. -1 can't equal anything squared.
Cardano used the impossible numbers anyway. He called them "sophistic" and "useless." But when he plugged them through his formula and they canceled out at the end, he got the right answer.
The impossible numbers worked.
Three centuries later, they became the foundation of quantum mechanics, signal processing, and electrical engineering. Today we call them complex numbers—though there's nothing complex about them once you see what they really are.
The Unlock
Here's what i = √(-1) actually means: it's not imaginary. It's perpendicular.
Real numbers live on a line. Complex numbers live on a plane. The "imaginary" part just points in a direction the real line can't reach—90 degrees away, into a second dimension.
Once you see this, everything clicks:
- Adding complex numbers is vector addition
- Multiplying complex numbers is rotation + scaling
- Euler's formula e^(iθ) = cos θ + i sin θ is just saying "exponentials and rotation are the same thing"
The name "imaginary" was a historical mistake. These numbers are as real as any other—they just live in two dimensions instead of one.
What This Series Covers
The Foundation:
- What Are Complex Numbers? — When real numbers aren't enough
- The Imaginary Unit i — Not imaginary, just perpendicular
- The Complex Plane — Numbers as points in 2D space
The Geometry:
- Polar Form — Every complex number as a magnitude and angle
- Euler's Formula — The equation that unifies exponentials and rotation
- Euler's Identity — When e, π, i, 1, and 0 meet in the most beautiful equation
The Power:
- Roots of Unity — Complex numbers that become 1 when powered
- Complex Conjugate — The mirror operation
- Synthesis — Why every polynomial finally factors completely
Why Complex Numbers Matter
- Quantum mechanics runs on complex numbers. Wavefunctions are complex. Probability amplitudes are complex. Without i, you can't write the Schrödinger equation.
- Electrical engineering uses them for AC circuits. Impedance is complex. Phase shifts are rotations in the complex plane.
- Signal processing treats signals as complex exponentials. The Fourier transform maps functions to complex amplitudes.
- Fluid dynamics, control theory, number theory—complex analysis appears everywhere.
The numbers that "shouldn't exist" turned out to be everywhere we looked.
This is the hub page for the Complex Numbers series, exploring the mathematics that extended algebra into two dimensions.
The Series



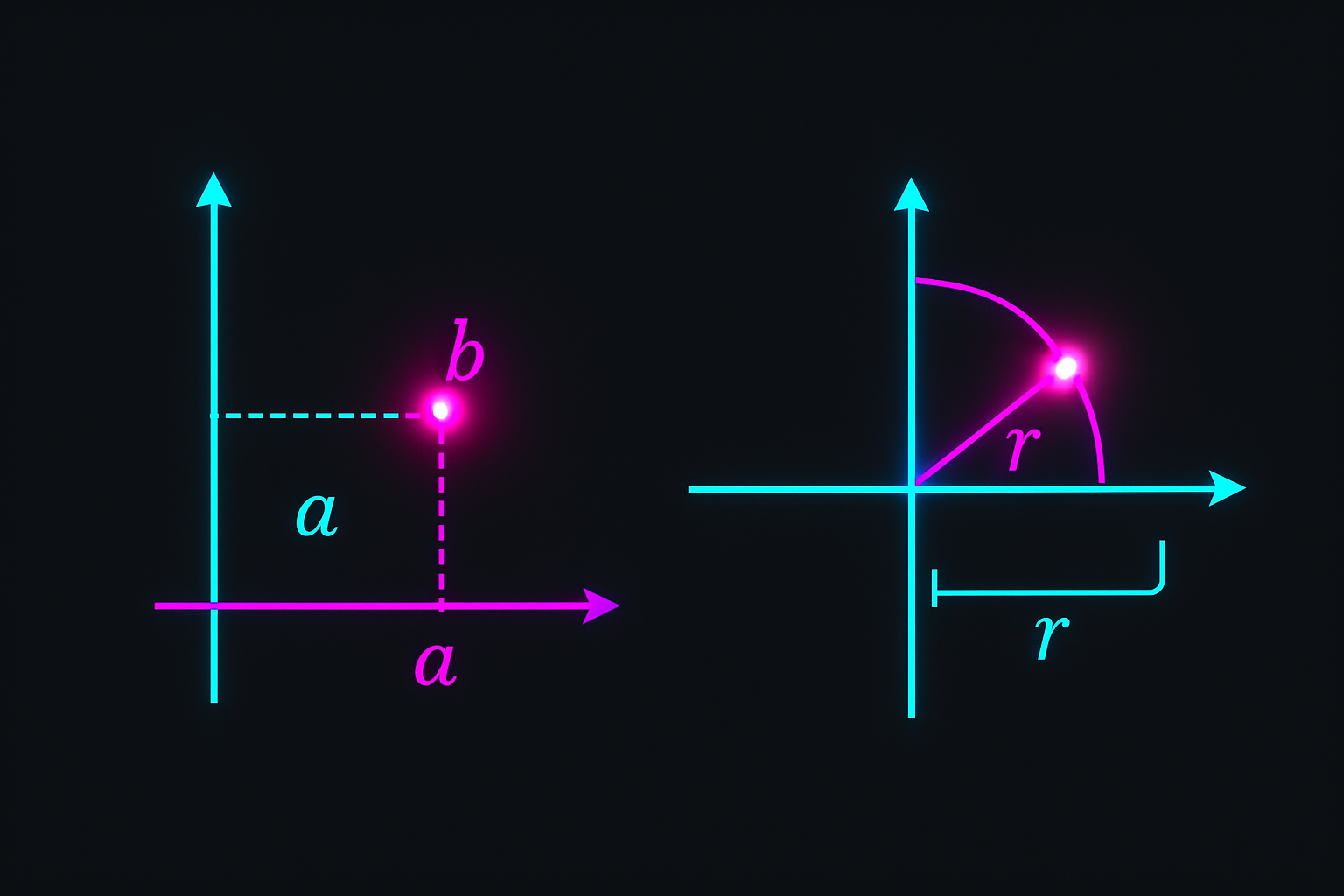
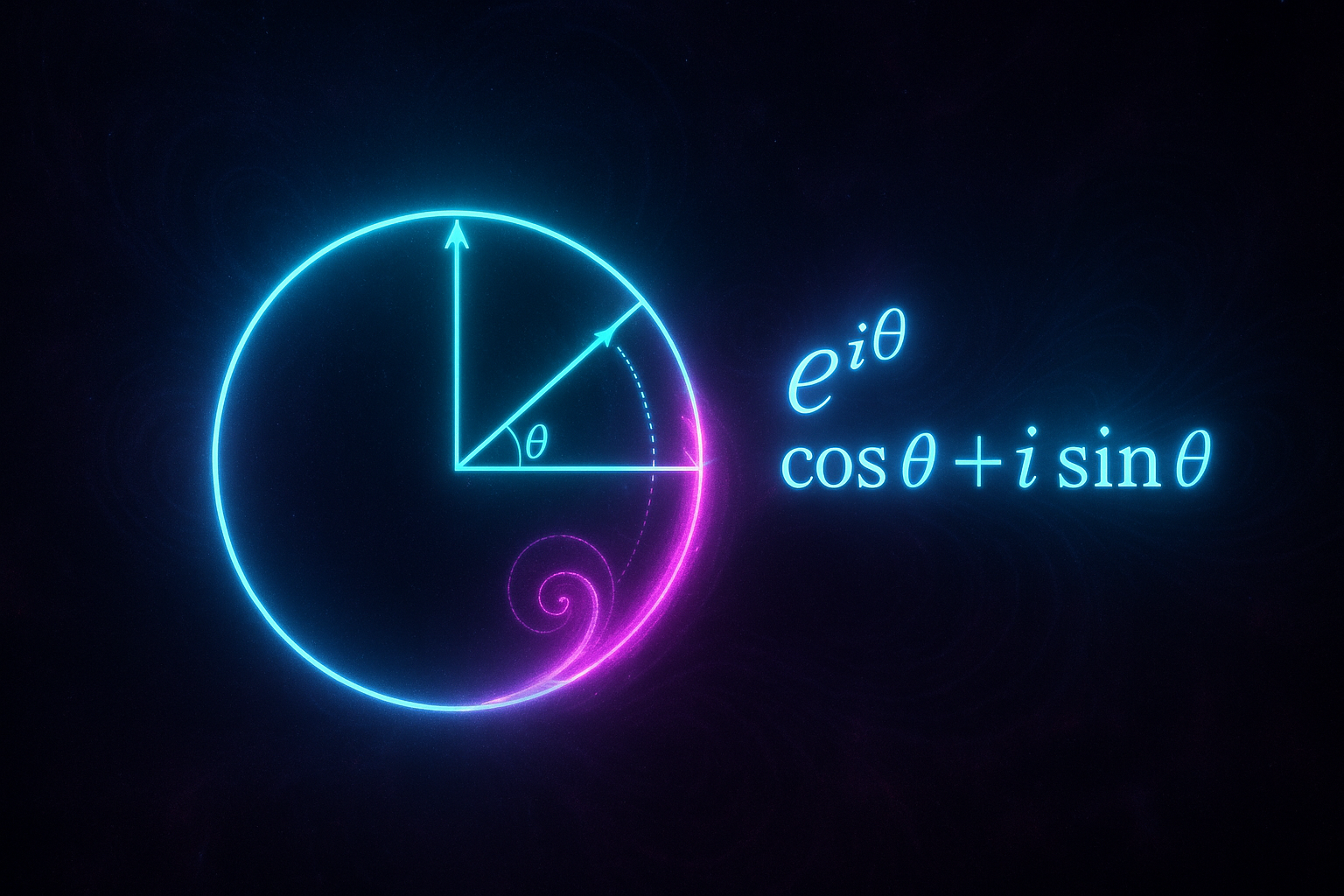



Comments ()