Polar Form: Complex Numbers as Rotation and Scaling
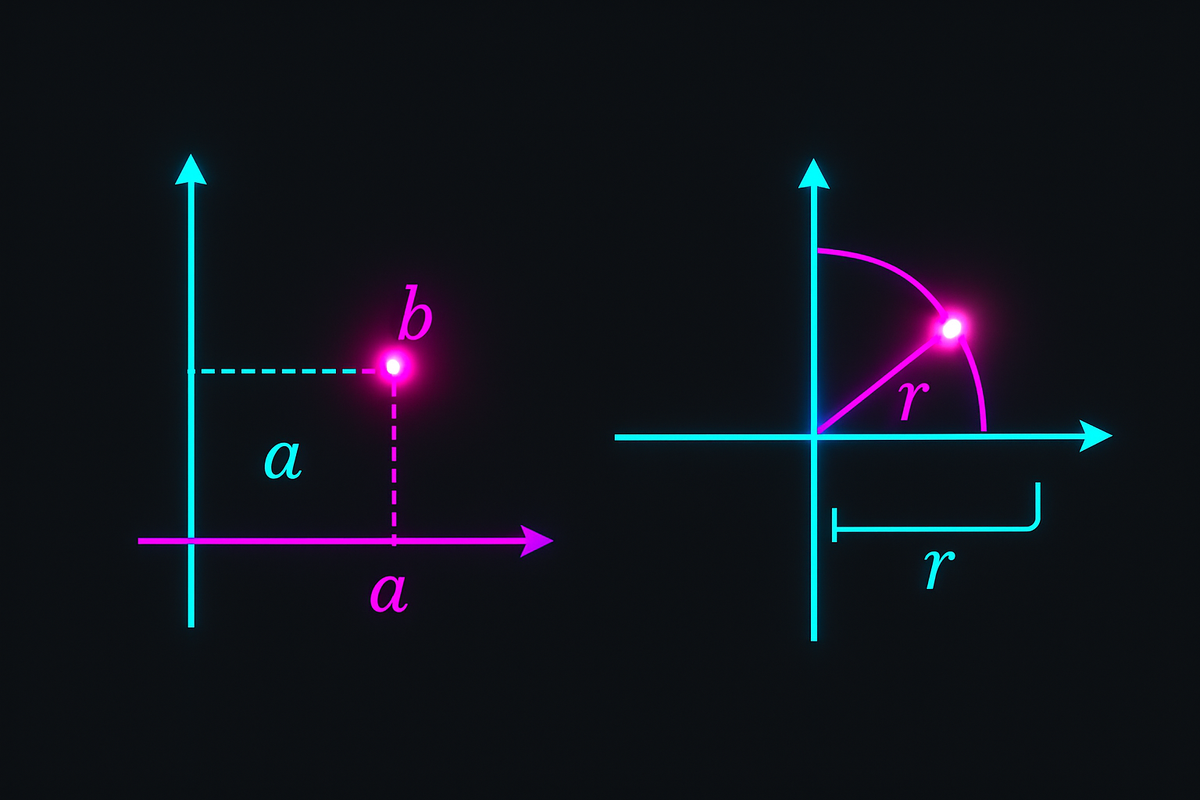
Every complex number can be described two ways:
Rectangular form: z = a + bi (go right a, up b) Polar form: z = r(cos θ + i sin θ) (go distance r at angle θ)
Rectangular is natural for addition. Polar is natural for multiplication.
Switch between them depending on what you're doing. The insight: complex multiplication is rotation combined with scaling.
The Polar Coordinates
For z = a + bi:
r = |z| = √(a² + b²) — the modulus, distance from origin
θ = arg(z) = arctan(b/a) — the argument, angle from positive real axis
Polar form:
z = r(cos θ + i sin θ)
Also written z = r cis θ or z = r∠θ (the angle notation).
Converting Between Forms
Rectangular to polar: Given z = a + bi:
- r = √(a² + b²)
- θ = arctan(b/a), adjusted for quadrant
Polar to rectangular: Given z = r cis θ:
- a = r cos θ
- b = r sin θ
- z = r cos θ + ir sin θ
Example: Convert 1 + i to polar.
- r = √(1² + 1²) = √2
- θ = arctan(1/1) = π/4
- z = √2 cis(π/4) = √2(cos π/4 + i sin π/4)
Example: Convert 2 cis(π/3) to rectangular.
- a = 2 cos(π/3) = 2 · (1/2) = 1
- b = 2 sin(π/3) = 2 · (√3/2) = √3
- z = 1 + √3 i
Why Polar Form Matters
Multiplication becomes simple.
For z₁ = r₁ cis θ₁ and z₂ = r₂ cis θ₂:
z₁ · z₂ = r₁r₂ cis(θ₁ + θ₂)
Multiply the moduli. Add the arguments.
In rectangular form, (a + bi)(c + di) = (ac - bd) + (ad + bc)i. Four multiplications, messy.
In polar form: multiply two numbers, add two angles. Clean.
Proof of the Multiplication Rule
z₁z₂ = r₁(cos θ₁ + i sin θ₁) · r₂(cos θ₂ + i sin θ₂)
= r₁r₂[(cos θ₁ cos θ₂ - sin θ₁ sin θ₂) + i(sin θ₁ cos θ₂ + cos θ₁ sin θ₂)]
= r₁r₂[cos(θ₁ + θ₂) + i sin(θ₁ + θ₂)]
= r₁r₂ cis(θ₁ + θ₂)
The angle addition formulas from trigonometry do the work.
Division in Polar Form
z₁ / z₂ = (r₁/r₂) cis(θ₁ - θ₂)
Divide the moduli. Subtract the arguments.
Example: (2 cis π/3) / (4 cis π/6) = (2/4) cis(π/3 - π/6) = (1/2) cis(π/6).
No conjugate multiplication needed.
Powers: De Moivre's Theorem
For any complex number z = r cis θ and integer n:
zⁿ = rⁿ cis(nθ)
Raise the modulus to the power. Multiply the argument by n.
This is De Moivre's Theorem.
Example: (1 + i)⁸
First convert: 1 + i = √2 cis(π/4)
(1 + i)⁸ = (√2)⁸ cis(8 · π/4) = 16 cis(2π) = 16 cis(0) = 16
Verify: computing (1+i)² = 2i, (2i)² = -4, (-4)² = 16. ✓
De Moivre makes high powers trivial.
Roots in Polar Form
The nth roots of z = r cis θ are:
ⁿ√z = ⁿ√r · cis((θ + 2πk)/n) for k = 0, 1, 2, ..., n-1
There are n distinct nth roots, evenly spaced around a circle.
Example: Find the cube roots of 8.
8 = 8 cis(0).
Cube roots: ³√8 · cis((0 + 2πk)/3) = 2 cis(2πk/3) for k = 0, 1, 2.
- k = 0: 2 cis(0) = 2
- k = 1: 2 cis(2π/3) = 2(-1/2 + i√3/2) = -1 + i√3
- k = 2: 2 cis(4π/3) = 2(-1/2 - i√3/2) = -1 - i√3
Three cube roots, forming an equilateral triangle.
The Geometric Picture
Multiplying z by w = r cis θ:
- Scales z by factor r
- Rotates z counterclockwise by angle θ
This is why i² = -1:
- i = cis(π/2) — angle 90°
- i² = cis(π) — angle 180°
- cis(π) = -1
Multiplying by i is a quarter turn.
Special Angles
| z | r | θ | Polar form |
|---|---|---|---|
| 1 | 1 | 0 | cis(0) |
| i | 1 | π/2 | cis(π/2) |
| -1 | 1 | π | cis(π) |
| -i | 1 | 3π/2 | cis(3π/2) |
| 1+i | √2 | π/4 | √2 cis(π/4) |
| √3+i | 2 | π/6 | 2 cis(π/6) |
Memorizing these helps with quick calculations.
Complex Exponential Preview
Euler's formula says:
e^(iθ) = cos θ + i sin θ
So polar form becomes:
z = r · e^(iθ)
This is the exponential form — even cleaner than cis notation.
Multiplication: r₁e^(iθ₁) · r₂e^(iθ₂) = r₁r₂ · e^(i(θ₁+θ₂))
The exponent rules apply directly. Angles add because exponents add.
Applications
Signal processing: Signals are represented as A·e^(iωt), where A is amplitude and ω is frequency. Operations become simple.
AC circuits: Impedance is complex. Polar form gives magnitude (resistance) and phase directly.
Quantum mechanics: Wave functions have phase. Polar form separates magnitude (probability amplitude) from phase.
Rotations: Any 2D rotation is multiplication by e^(iθ). Rotation matrices reduce to complex multiplication.
The Principal Argument
The argument θ is only defined up to multiples of 2π. Adding 2π gives the same point.
The principal argument Arg(z) restricts θ to a standard range:
- Usually (-π, π] or [0, 2π)
This makes θ unique (except for z = 0, which has no well-defined argument).
Summary
Polar form: z = r cis θ = r(cos θ + i sin θ) = re^(iθ)
Modulus: r = |z| = distance from origin Argument: θ = arg(z) = angle from positive real axis
Operations:
- Multiply: multiply moduli, add arguments
- Divide: divide moduli, subtract arguments
- Power: raise modulus to power, multiply argument by power
- Roots: take root of modulus, divide argument by root degree (n roots)
Polar form reveals the geometry. Multiplication is rotation and scaling.
Further Reading
- Needham, T. Visual Complex Analysis. Geometric foundations.
- Nahin, P. An Imaginary Tale. Historical development.
- Marsden, J. Basic Complex Analysis. Undergraduate text.
This is Part 4 of the Complex Numbers series. Next: "Euler's Formula" — the equation that unifies exponentials and rotation.
Part 4 of the Complex Numbers series.
Previous: The Complex Plane: Numbers as Points in Two Dimensions Next: Euler's Formula: The Most Beautiful Equation in Mathematics
Comments ()