The Exponential Function eˣ: The Most Important Function in Mathematics
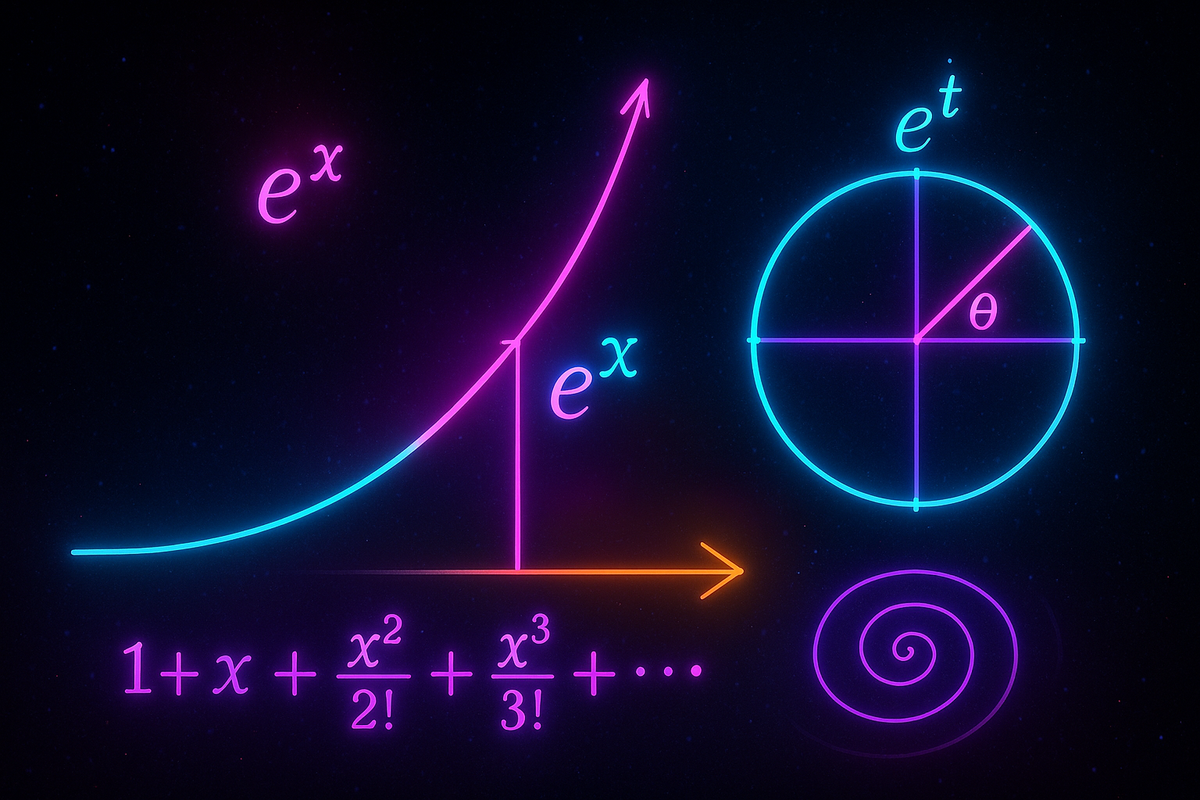
eˣ is the function that equals its own derivative.
That's not just a curious property—it's the defining property. Among all possible functions, only one is unchanged by differentiation. That function is eˣ (and its constant multiples).
This makes eˣ the fixed point of calculus. Differentiate it: you get eˣ. Integrate it: you get eˣ. The function that stays exactly where it is.
Why does this matter? Because the rate of change equaling the current value describes natural growth. Populations, investments, nuclear reactions—whenever change is proportional to amount, eˣ appears.
The Definition
The exponential function can be defined multiple ways:
Definition 1: Power series
eˣ = ∑(xⁿ/n!) = 1 + x + x²/2! + x³/3! + x⁴/4! + ...
Definition 2: Limit
eˣ = lim(n→∞) (1 + x/n)ⁿ
Definition 3: Differential equation
eˣ is the solution to dy/dx = y with y(0) = 1.
Definition 4: Inverse
eˣ is the inverse of ln(x).
All definitions are equivalent. Each highlights a different aspect of what makes eˣ special.
The Derivative Property
d/dx(eˣ) = eˣ
Proof from the series:
d/dx(1 + x + x²/2! + x³/3! + ...) = 0 + 1 + 2x/2! + 3x²/3! + ... = 1 + x + x²/2! + ... = eˣ
Each term's derivative produces the previous term. The series regenerates itself.
This is unique. For any other base b:
d/dx(bˣ) = bˣ × ln(b)
Only when b = e does the extra factor disappear.
The Graph
The graph of y = eˣ has these features:
- Passes through (0, 1)
- Always positive
- Increasing everywhere
- Concave up everywhere
- Horizontal asymptote y = 0 as x → -∞
- Grows faster than any polynomial as x → +∞
At any point, the slope equals the height. The steeper it gets, the faster it rises.
At x = 0: height 1, slope 1. At x = 1: height e ≈ 2.718, slope e ≈ 2.718. At x = 2: height e² ≈ 7.389, slope e² ≈ 7.389.
The function climbs a ladder of its own making.
Key Values
| x | eˣ |
|---|---|
| -2 | 0.135 |
| -1 | 0.368 |
| 0 | 1 |
| 1 | 2.718 |
| 2 | 7.389 |
| 5 | 148.4 |
| 10 | 22,026 |
eˣ grows extremely fast. By x = 10, it's over 22,000. By x = 100, it's a number with 44 digits.
For negative x, eˣ → 0 but never reaches it.
Properties
e⁰ = 1 (by definition)
eᵃ × eᵇ = e^(a+b) (exponent addition rule)
eᵃ / eᵇ = e^(a-b) (exponent subtraction)
(eᵃ)ᵇ = e^(ab) (power of a power)
e⁻ˣ = 1/eˣ (reciprocal)
eˣ × e⁻ˣ = e⁰ = 1 (inverse)
These are the standard exponent rules, but they hold because of how eˣ is constructed.
eˣ and Differential Equations
The equation dy/dx = ky has solution y = Ce^(kx).
This is THE equation of proportional change:
- k > 0: exponential growth
- k < 0: exponential decay
Every process where the rate of change is proportional to the current value follows this pattern:
Population growth: dP/dt = rP → P = P₀e^(rt)
Radioactive decay: dN/dt = -λN → N = N₀e^(-λt)
Compound interest: dA/dt = rA → A = A₀e^(rt)
Newton's cooling: dT/dt = -k(T - Tₐ) → T = Tₐ + (T₀-Tₐ)e^(-kt)
The exponential function is why these all have the same mathematical form.
Complex Exponentials
When x is complex, eˣ still works. For x = iθ (purely imaginary):
e^(iθ) = cos(θ) + i·sin(θ) (Euler's formula)
This connects exponentials to trigonometry. Rotation in the complex plane is exponentiation.
Special case θ = π:
e^(iπ) = cos(π) + i·sin(π) = -1 + 0 = -1
Hence: e^(iπ) + 1 = 0, Euler's identity.
Complex exponentials unify two seemingly different branches of mathematics.
The Exponential Function and Area
The area under eˣ from -∞ to x equals eˣ itself.
∫₋∞ˣ eᵗ dt = eˣ
The accumulated area up to any point equals the height at that point.
This is another manifestation of the self-referential nature of eˣ.
Taylor Series
Around x = 0:
eˣ = 1 + x + x²/2! + x³/3! + x⁴/4! + ...
This series converges for all x, not just near 0. The exponential function is entire—analytic everywhere.
The series lets you compute eˣ to arbitrary precision:
e^1 = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + ...
After 10 terms, you get e ≈ 2.718281801 (correct to 6 decimal places).
Connection to Other Exponentials
Any exponential bˣ can be written using e:
bˣ = e^(x ln b)
Since b = e^(ln b), we have:
bˣ = (e^(ln b))ˣ = e^(x ln b)
This is why eˣ is the "universal" exponential. All others are just scaled versions.
d/dx(bˣ) = d/dx(e^(x ln b)) = ln(b) × e^(x ln b) = ln(b) × bˣ
The ln(b) factor appears because bˣ is eˣ with a different scale.
Inverse: The Natural Logarithm
If y = eˣ, then x = ln(y).
The natural log undoes exponentiation:
ln(eˣ) = x and e^(ln x) = x
Together they form an inverse pair:
- eˣ: horizontal stretch becomes vertical
- ln(x): vertical stretch becomes horizontal
Why eˣ Is Fundamental
- Fixed point of differentiation. The only function unchanged by taking derivatives.
- Solution to natural growth. dy/dx = y has solution eˣ.
- Universal exponential. All other exponentials are eˣ in disguise.
- Connects to trigonometry. e^(iθ) = cos θ + i sin θ.
- Analytic everywhere. The Taylor series converges for all x.
- Foundation of calculus. Integration, differential equations, transforms—eˣ is inescapable.
The exponential function isn't just one function among many. It's the function that is its own rate of change—the mathematical expression of pure, proportional growth.
Part 6 of the Exponential Functions series.
Previous: Compound Interest: Exponential Growth in Finance Next: Exponential vs Polynomial Growth: Why Exponentials Always Win
Comments ()