Synthesis: Exponentials as the Language of Multiplicative Processes

Exponential functions describe anything that grows by percentages.

This is the core insight. When change is proportional to current value—when you grow by multiplying rather than adding—you're in exponential territory.

Linear growth adds the same amount each step. Exponential growth multiplies by the same factor. The difference sounds subtle. It's profound.

Think of a savings account versus an investment account. Saving $100 per month is linear—after 10 years you have $12,000 of contributions. But an investment growing at 7% annually is exponential—that same $12,000 invested becomes roughly $17,000 because each year's gains generate the next year's gains.

The power of exponentials isn't in any single step. It's in the accumulation of multiplicative steps, each building on the last.

The Unifying Equation

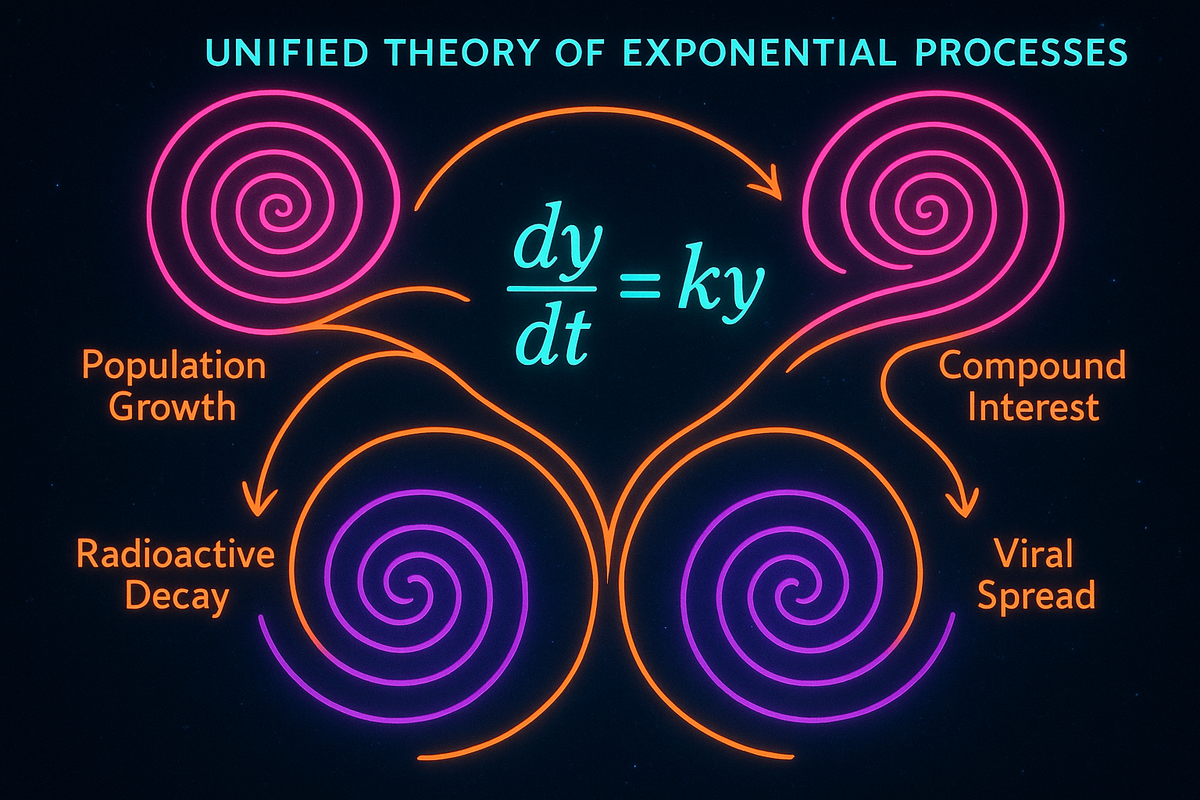
Every exponential process obeys:

dy/dt = ky

The rate of change (dy/dt) is proportional (k) to the current value (y).

Solution: y = y₀e^(kt)

This single equation describes:

• Population growth (more individuals → more births)
• Radioactive decay (more atoms → more decays)
• Compound interest (more money → more interest)
• Viral spread (more infected → more infections)
• Cooling (bigger temperature difference → faster heat flow)

The mathematics is the same. Only the interpretation changes.

Three Behaviors

k > 0: Exponential growth The quantity explodes. Doubling time = ln(2)/k ≈ 0.693/k.

k < 0: Exponential decay The quantity shrinks toward zero. Half-life = ln(2)/|k|.

k = 0: Constant Nothing changes. The trivial case.

The sign of k determines everything.

Why e?

The number e ≈ 2.71828 appears because it makes calculus clean.

d/dx(eˣ) = eˣ

This is unique. No other function equals its own derivative. The function eˣ is the fixed point of differentiation—the mathematical expression of perfect proportional growth.

Other bases work (2ˣ, 10ˣ), but they introduce extra factors. e is the natural base because it's what continuous compounding naturally produces.

The Hierarchy

Exponentials dominate polynomials. Always. Eventually.

x¹⁰⁰⁰ < 1.001ˣ for large enough x.

This matters for:

• Algorithm complexity (exponential = intractable)
• Long-term investment (compound beats linear)
• Anything where "just a few more doublings" applies

The dominance of exponentials over polynomials is why multiplicative processes are so powerful—and so dangerous.

What We Learned

1. Exponential functions have the variable in the exponent. f(x) = bˣ, not f(x) = xᵇ.
2. Exponential growth doubles repeatedly. The doubling time is constant; the amount doubled grows each time.
3. Exponential decay halves repeatedly. It approaches zero but never reaches it.
4. e is the natural base. Continuous compounding, differential equations, and calculus all prefer e.
5. Compound interest is exponential growth in finance. Time matters more than rate.
6. eˣ equals its own derivative. The most special function in mathematics.
7. Exponentials beat polynomials. Multiplicative growth eventually dominates additive growth.

The Deep Pattern

Exponential functions capture feedback loops.

When output feeds back into input—when growth accelerates growth, or decay accelerates decay—you get exponentials.

This is why exponentials appear everywhere in nature and society. Any self-reinforcing process is exponential at its core.

• More people → more births → more people
• More capital → more returns → more capital
• More infections → more transmissions → more infections
• More decay → less material → slower decay (negative feedback)

The mathematics of feedback is the mathematics of eˣ.

Positive feedback amplifies: the system spirals toward infinity (or a resource limit). Epidemics, viral content, nuclear chain reactions.

Negative feedback dampens: the system spirals toward equilibrium. Cooling objects, draining capacitors, drug clearance from blood.

Both follow the same equation dy/dt = ky. The sign of k determines whether you spiral up or spiral down.

Understanding exponentials means understanding feedback. Systems without feedback grow linearly or stay constant. Systems WITH feedback are where exponentials live.

Recognizing Exponential Processes

How do you know if something is exponential in the wild?

The doubling test: Is there a constant doubling time? If a quantity doubles every 7 years, or every 3 hours, or every 6 months—regardless of how large it already is—that's exponential.

The percentage test: Is growth expressed as a percentage? "5% annual growth" is exponential. "Growing by 100 units per year" is linear.

The ratio test: Take consecutive measurements. Is the ratio roughly constant? If y₂/y₁ ≈ y₃/y₂ ≈ y₄/y₃, you have exponential behavior.

The log-linear test: Plot the data with a logarithmic y-axis. If it looks like a straight line, the underlying process is exponential. The slope tells you the growth rate.

Conversely, if the doubling time keeps changing, if growth is in absolute amounts, if ratios vary—it's probably not exponential. Many S-curves look exponential early but are actually logistic (they level off).

Intuition Check

The human brain evolved for linear thinking. We estimate:

• How far is it? (linear distance)
• How long will it take? (linear time)
• How many are there? (linear count)

Exponential intuition doesn't come naturally. We systematically underestimate:

• How fast compound interest grows
• How quickly epidemics spread
• How enormous 2⁶⁴ really is

Building exponential intuition means internalizing:

• Doubling time matters more than current size
• The last doubling adds as much as all previous doublings combined
• Early intervention on exponential problems is dramatically easier than late intervention

The Lily Pad Revisited

A lily pad doubles daily and covers the pond on day 30.

When is it half-covered? Day 29. When is it 1% covered? Day 23. When is it barely visible (0.1%)? Day 20.

For 20 days, you'd barely notice. Then 10 more days and it's everywhere. That's exponential growth: invisible until it's unavoidable.

When Exponentials Break Down

Pure exponential growth can't last forever. Here's where the model fails:

Resource limits: Bacteria can't grow exponentially forever—they run out of food. Populations hit carrying capacity. Investment returns diminish at scale. Most "exponential" growth is really the early phase of a logistic curve.

Saturation: A viral video can only reach so many people. Once everyone who might watch has watched, growth stops. Exponentials assume an infinite pool; reality has boundaries.

Intervention: Epidemics don't grow exponentially forever because people change behavior. Interest rates change, disrupting compound growth. Technology creates discontinuities that break exponential trends.

Model breakdown: Some processes look exponential over certain ranges but aren't fundamentally exponential. Be wary of extrapolating.

The power of exponential models is in the early and middle phases—when feedback is still positive and resources haven't constrained growth. The wisdom is knowing when the model applies and when it doesn't.

Beyond Growth and Decay

Exponentials connect to:

• Complex numbers: e^(iθ) = cos θ + i sin θ (Euler's formula)
• Fourier analysis: Signals as sums of complex exponentials
• Probability: The normal distribution involves e^(-x²)
• Quantum mechanics: Wave functions evolve as e^(-iHt/ℏ)

The exponential function isn't just about growth. It's a fundamental building block of mathematics, connecting algebra, calculus, and geometry.

Euler's formula alone shows how deep this goes. The exponential function, when given an imaginary argument, produces rotation. This means oscillation (sines and cosines) and growth/decay (exponentials) are the same thing in disguise—just different projections of spiral motion in the complex plane.

This is why eˣ is called the most important function in mathematics. It doesn't just describe growth. It unifies the behavior of waves, rotations, oscillations, and decay into a single framework.

How the Pieces Fit Together

This series explored exponentials from multiple angles. Here's how they connect:

The foundation: What is an exponential function? It's bˣ—the variable in the exponent. This creates multiplicative growth.

The behavior: Exponential growth and decay are two sides of the same coin. Growth has k > 0 (doubling times). Decay has k < 0 (half-lives). Same equation, different signs.

The number e: Why e ≈ 2.718? Because it's what emerges from continuous compounding, and it makes d/dx(eˣ) = eˣ. The base that calculus prefers.

The application: Compound interest shows exponentials in finance—time in the market beats timing the market because compounding rewards patience.

The function eˣ: The pure case. Its own derivative, its own integral, the solution to dy/dt = y. The mathematical expression of "rate equals amount."

The comparison: Exponentials always beat polynomials. Multiplicative beats additive. This explains why exponential algorithms are intractable and why compound growth is so powerful.

Each piece reinforces the others. The definition leads to the properties. The properties explain the applications. The applications reveal why this matters.

The Takeaway

Exponential functions are the language of multiplicative processes—anything that grows by percentages rather than amounts.

They're counterintuitive, powerful, and everywhere. Master them, and you understand compound interest, epidemics, algorithm complexity, and the deep structure of continuous change.

The exponential function says: when growth feeds on itself, everything changes.

Additive growth is predictable. Each step adds the same amount. You can see where you'll be in 10 steps, 100 steps, 1000 steps.

Exponential growth is deceptive. The first 20 doublings look small. Then a few more doublings, and suddenly the quantity dominates everything. The lily pad covers the pond. The pandemic sweeps the globe. The investment dwarfs the contributions.

Understanding exponentials means understanding that the future can be qualitatively different from the past—not just "more of the same" but a phase transition into overwhelming. It's the math of compound effects, feedback loops, and the surprising power of steady multiplicative growth.

Once you see exponentials, you see them everywhere. And once you understand them, you're better equipped to harness their power and anticipate their dangers.

Part 8 of the Exponential Functions series.

Previous: Exponential vs Polynomial Growth: Why Exponentials Always Win