Integrals Explained

Integrals Explained | Ideasthesia

Archimedes wanted to find the area of a parabolic segment. No formula existed. So he did something brilliant: he filled the curve with triangles. Then smaller triangles. Then smaller still. As the triangles got infinitely small and infinitely numerous, their total area approached the exact answer.

Twenty centuries later, Newton and Leibniz turned this into calculus. The integral.

The integral is mathematics' answer to: how do you add up infinitely many infinitely small things?

It sounds impossible. But when the things you're adding shrink as fast as their number grows, you get finite answers. The area under a curve. The total distance traveled. The accumulated mass, charge, probability, or work.

Derivatives tell you how fast. Integrals tell you how much total. They're inverses—calculus's yin and yang.

The Core Insight

Here's what integration actually does: it reassembles a whole from its rates of change.

If velocity tells you how fast position changes, then integrating velocity gives you total position change. If power tells you how fast energy transfers, integrating power gives you total energy. If a probability density tells you how likely each value is, integrating it gives you the total probability.

The integral undoes the derivative. The Fundamental Theorem of Calculus makes this precise:

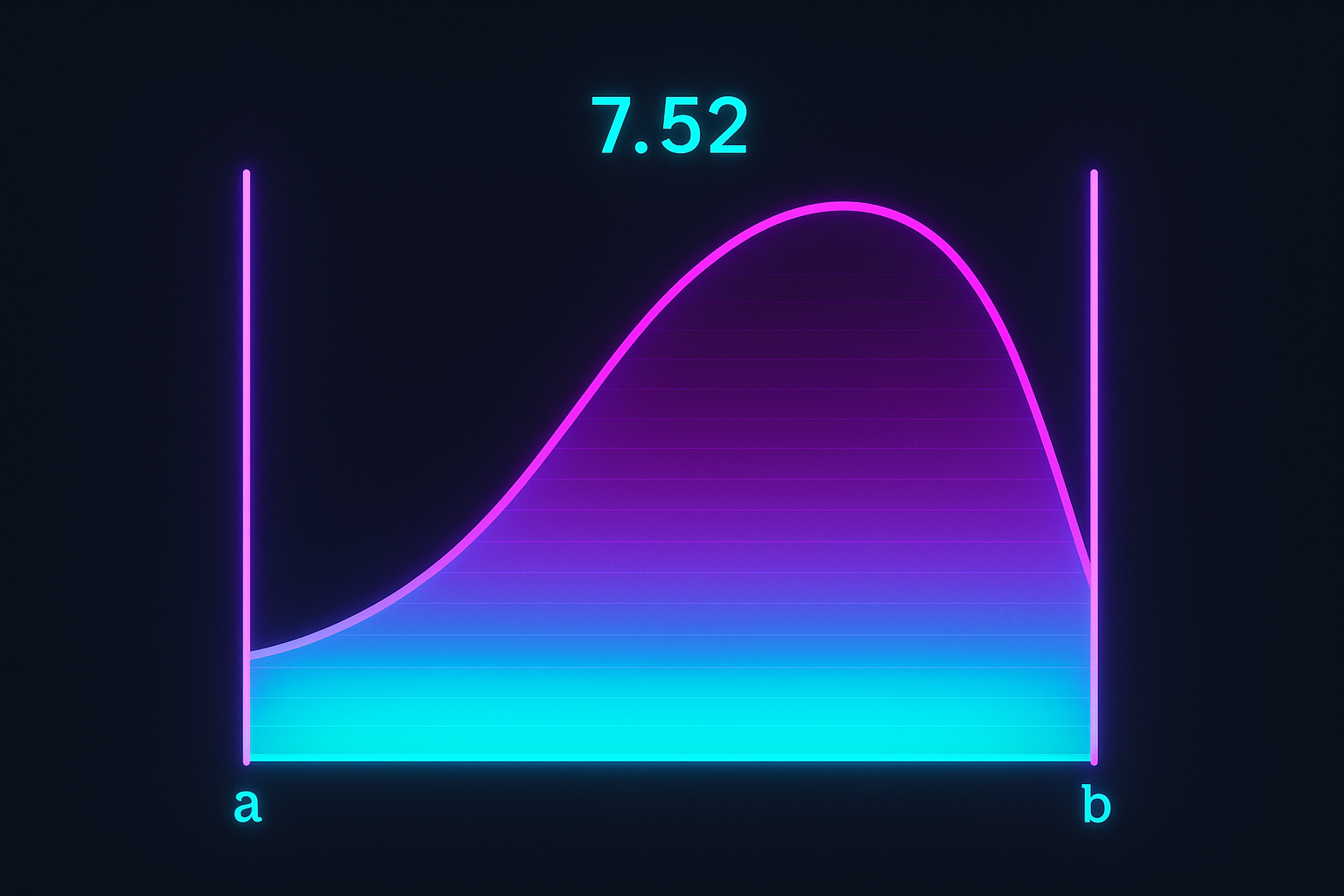
∫ₐᵇ f'(x) dx = f(b) - f(a)

The integral of a rate equals the net change. That single equation connects slopes to areas, rates to totals, instantaneous to cumulative.

What This Series Covers

The Foundation:

What Is an Integral? — Accumulation through infinite sums
The Fundamental Theorem of Calculus — Why differentiation and integration are opposites
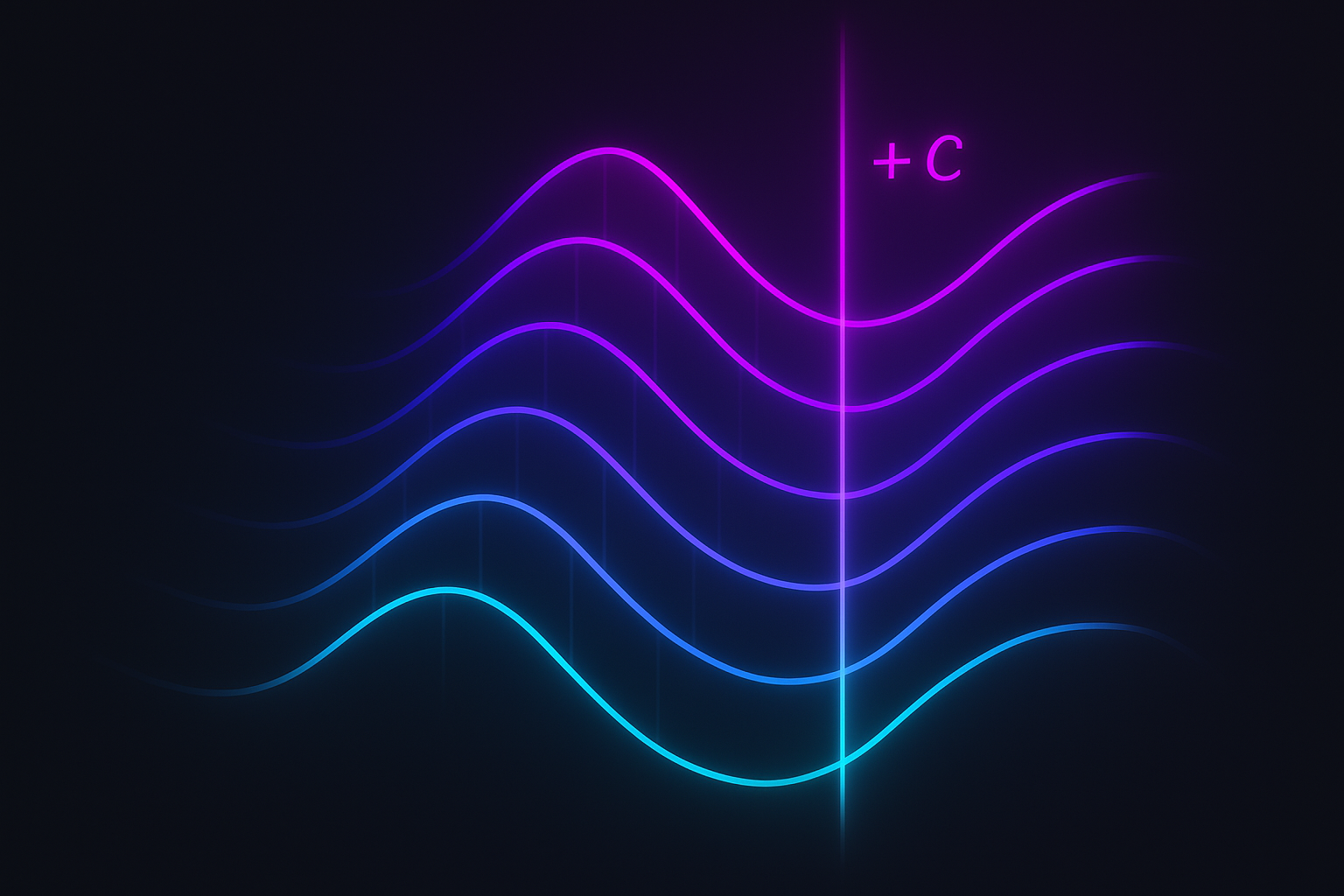
Antiderivatives — Finding functions from their derivatives

The Techniques:

Definite vs. Indefinite Integrals — Numbers versus families of functions
U-Substitution — The chain rule in reverse
Integration by Parts — The product rule in reverse
Improper Integrals — When infinity gets involved

The Applications:

Area Under Curves — The original motivation
Volumes of Revolution — Spinning curves into solids
Applications — Work, probability, center of mass, arc length
Synthesis — Integration as the language of accumulation

Where Integration Matters

Physics: Work is force integrated over distance. Impulse is force integrated over time.
Probability: The probability of an event is the integral of the density function.
Economics: Consumer surplus is an integral. Present value is an integral.
Engineering: Total charge, total flow, total signal energy—all integrals.

Anywhere you need a total from rates, integration is the tool.

This is the hub page for the Integrals series, exploring the mathematics of accumulation and totals.