Logarithms Explained
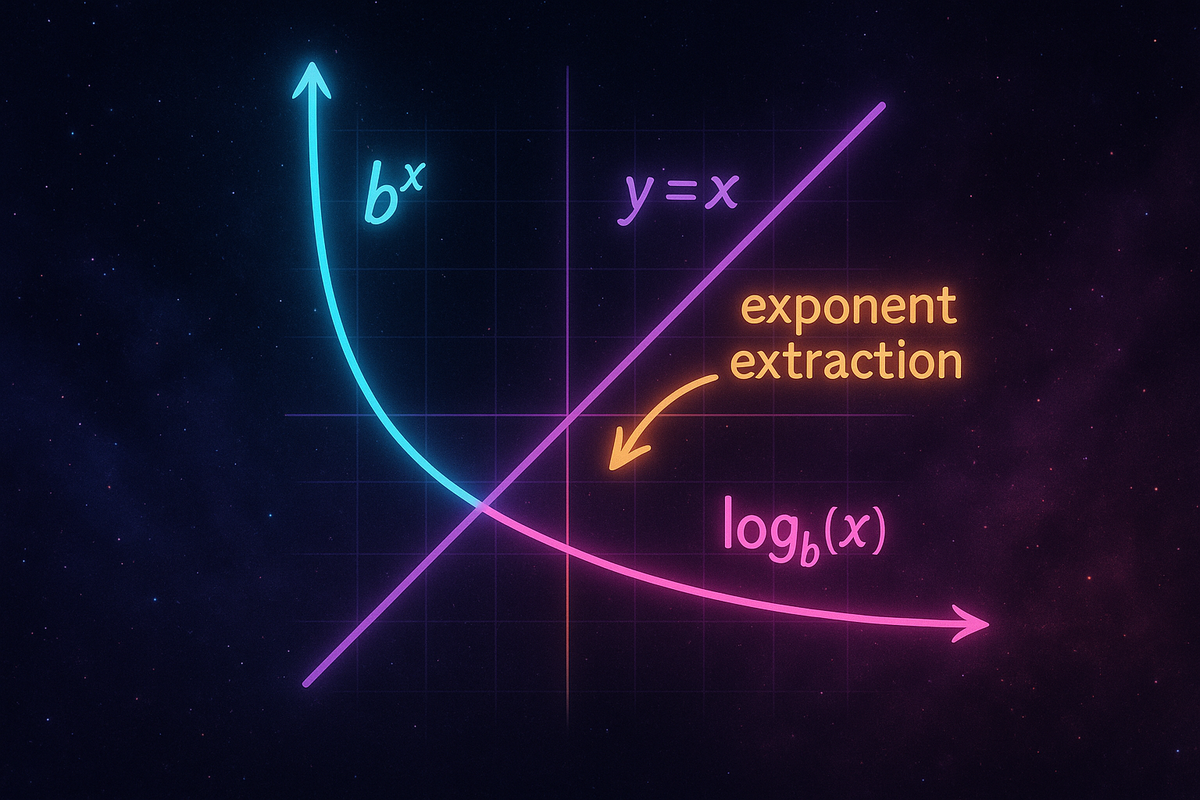
In 1614, John Napier published a book that would save astronomers decades of their lives.
The problem was multiplication. Astronomers spent hours multiplying large numbers by hand—computing planetary positions, navigation tables, financial projections. A single multiplication could take minutes. An error meant starting over.
Napier's invention: a table that converted multiplication into addition. Look up two numbers, add them together, look up the result. What took hours now took seconds.
He called it a "logarithm"—from Greek logos (ratio) and arithmos (number). The ratios that count.
Logarithms turn multiplication into addition. That's the whole trick. And it turns out this trick appears everywhere—from how we perceive sound to how we measure information to why compound interest is dangerous.
The Core Insight
A logarithm answers: what exponent gives this result?
- log₂(8) = 3 because 2³ = 8
- log₁₀(1000) = 3 because 10³ = 1000
- ln(e) = 1 because e¹ = e
The logarithm extracts the exponent. If exponentiation is "repeated multiplication," then logarithm is "how many times did we multiply?"
This reversal is why logarithms convert between operations:
- Multiplication → Addition: log(a × b) = log(a) + log(b)
- Division → Subtraction: log(a ÷ b) = log(a) - log(b)
- Powers → Multiplication: log(aⁿ) = n × log(a)
Every exponential relationship becomes linear through the logarithm.
What This Series Covers
The Basics:
- What Is a Logarithm? — The inverse of exponentiation
- Log Rules — Why multiplication becomes addition
- Common Logarithms — Base 10 and orders of magnitude
- Natural Logarithm — Why ln uses base e
The Applications:
- Change of Base — Converting between logarithm systems
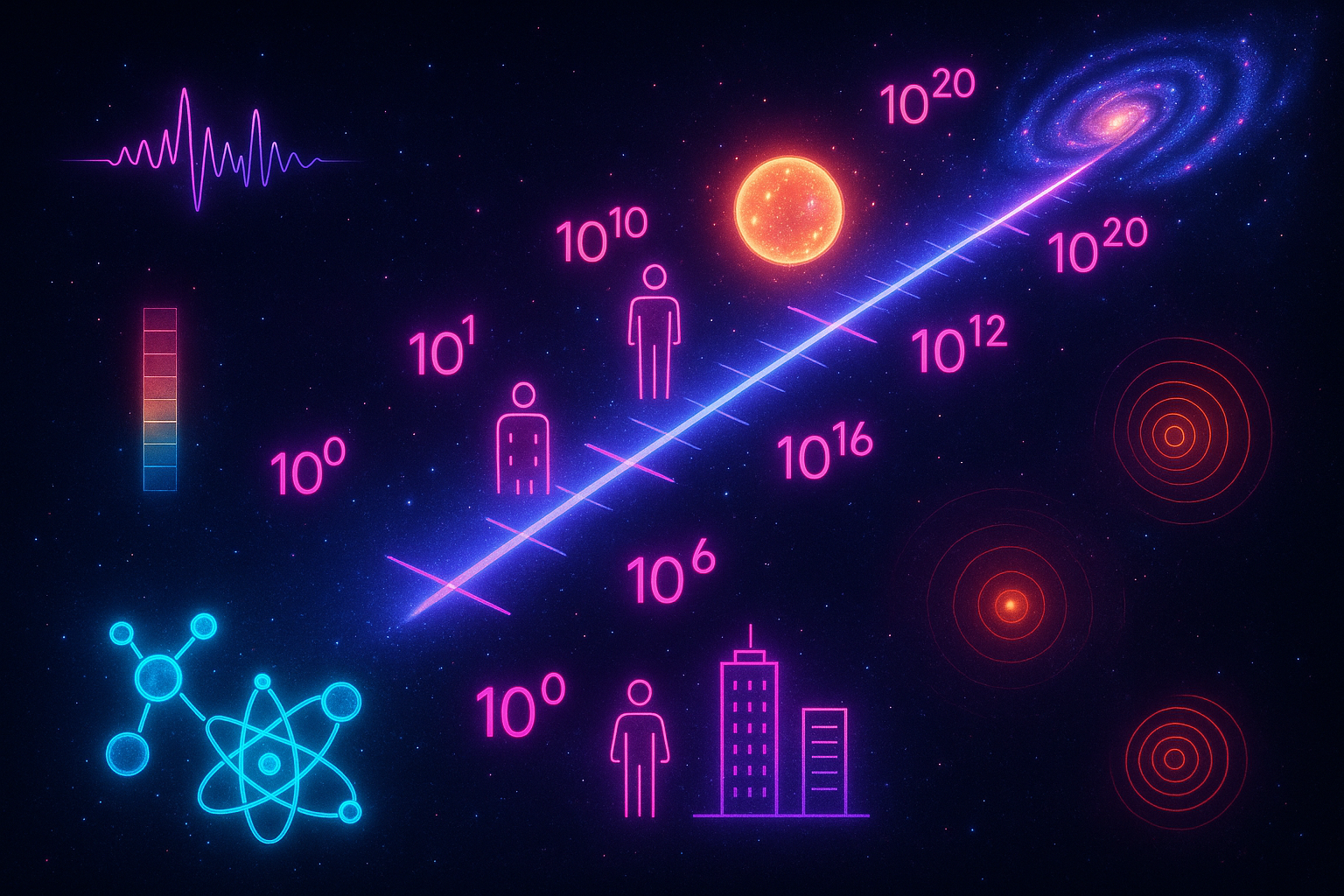
- Logarithmic Scales — Decibels, Richter, pH: when data spans many orders of magnitude
- Logarithms and Information — Why entropy and information use log
- Synthesis — Logarithms as the language of growth and scale
Where Logarithms Hide
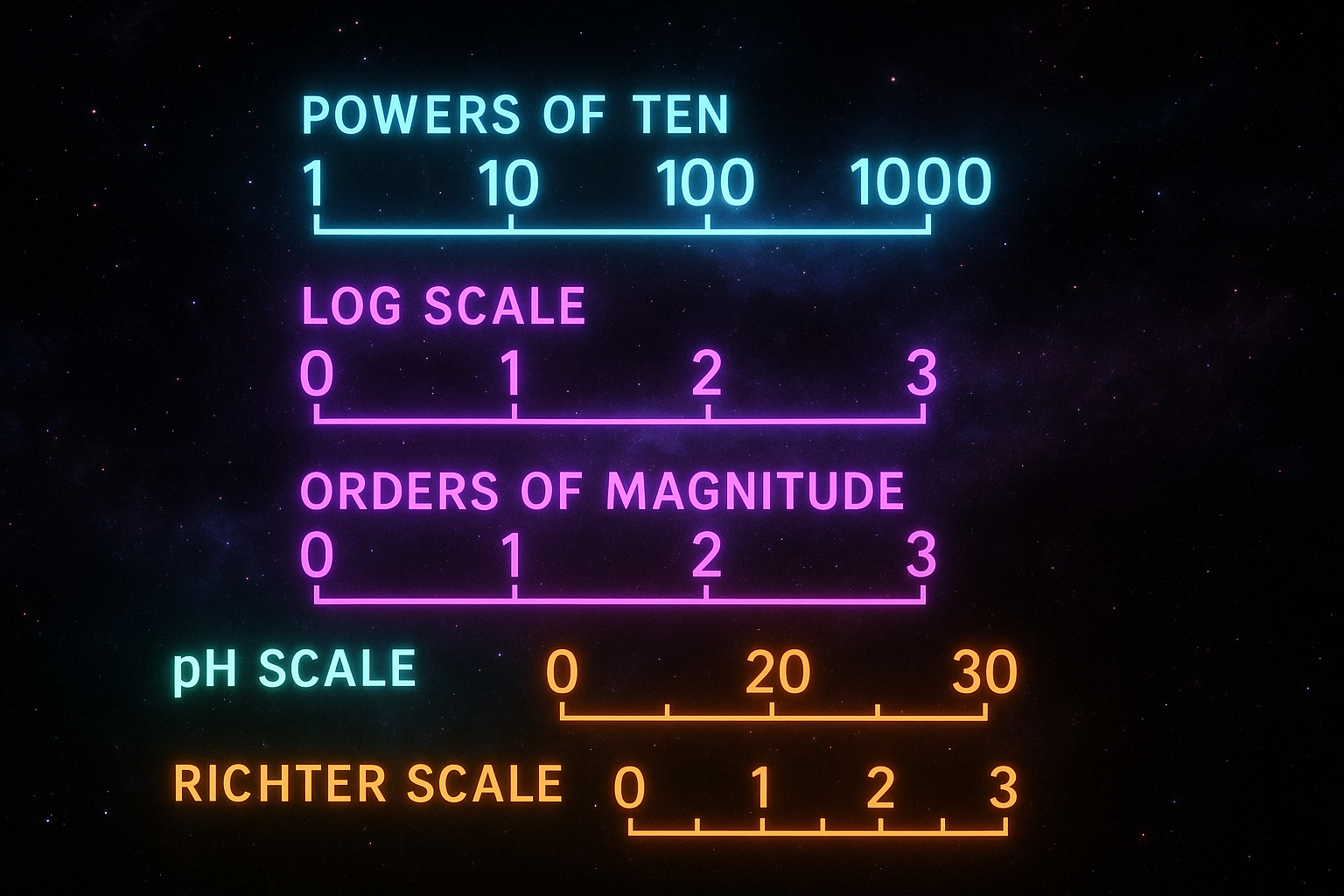
Sound is measured in decibels—a logarithmic scale. A 10 dB increase means 10× more power, not 10 units more.
Earthquakes use the Richter scale—logarithmic. A magnitude 6 is 10× more powerful than magnitude 5, and 100× more than magnitude 4.
Information is measured in bits—logarithms base 2. How many yes/no questions to find an item? That's log₂(n).
Perception is logarithmic. Doubling the brightness doesn't look twice as bright. The Weber-Fechner law says perception scales with the log of stimulus intensity.
Logarithms are how mathematics handles quantities that span many orders of magnitude—and how our own senses work.
This is the hub page for the Logarithms series, exploring the mathematics that transforms exponential relationships into linear ones.
The Series
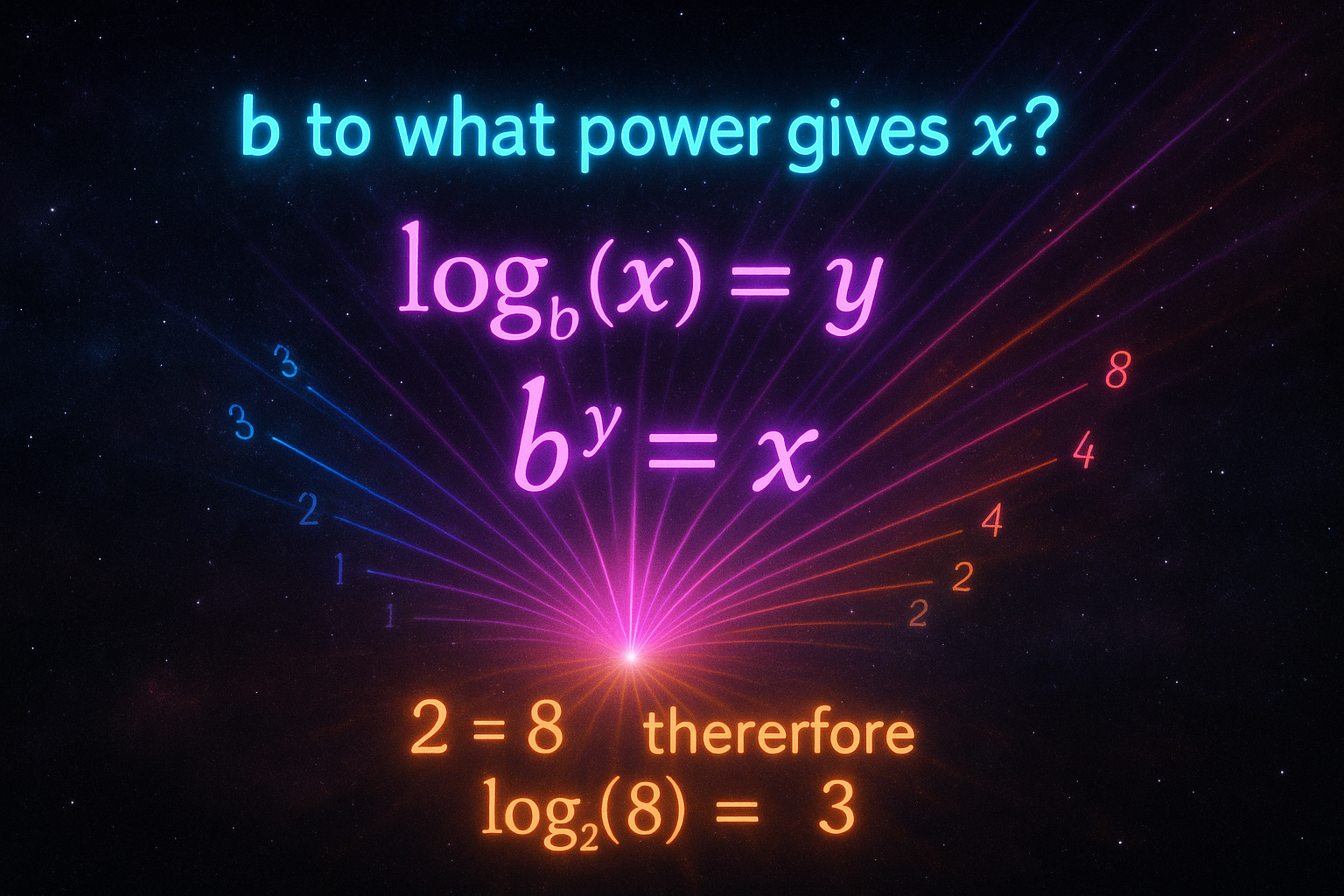
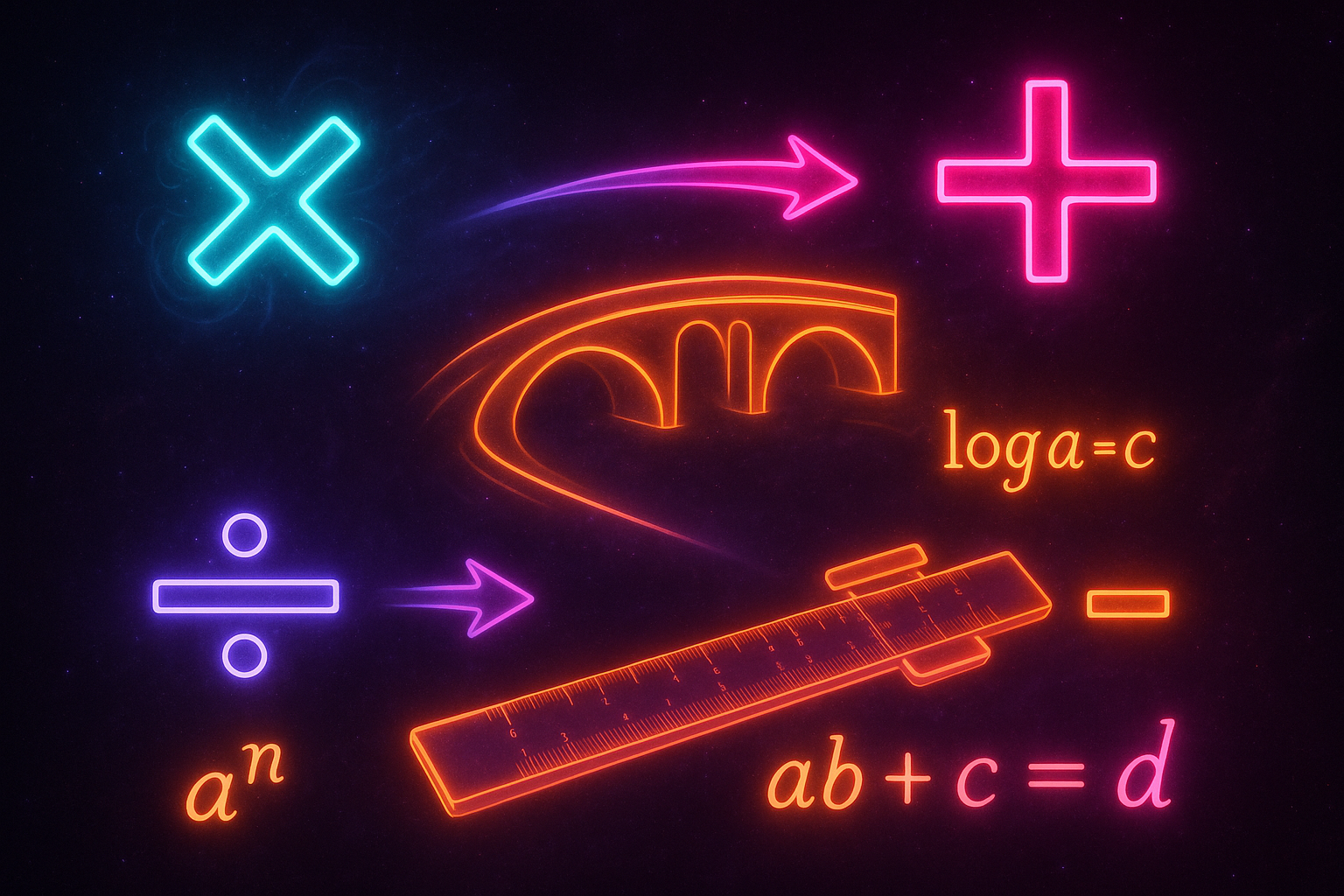
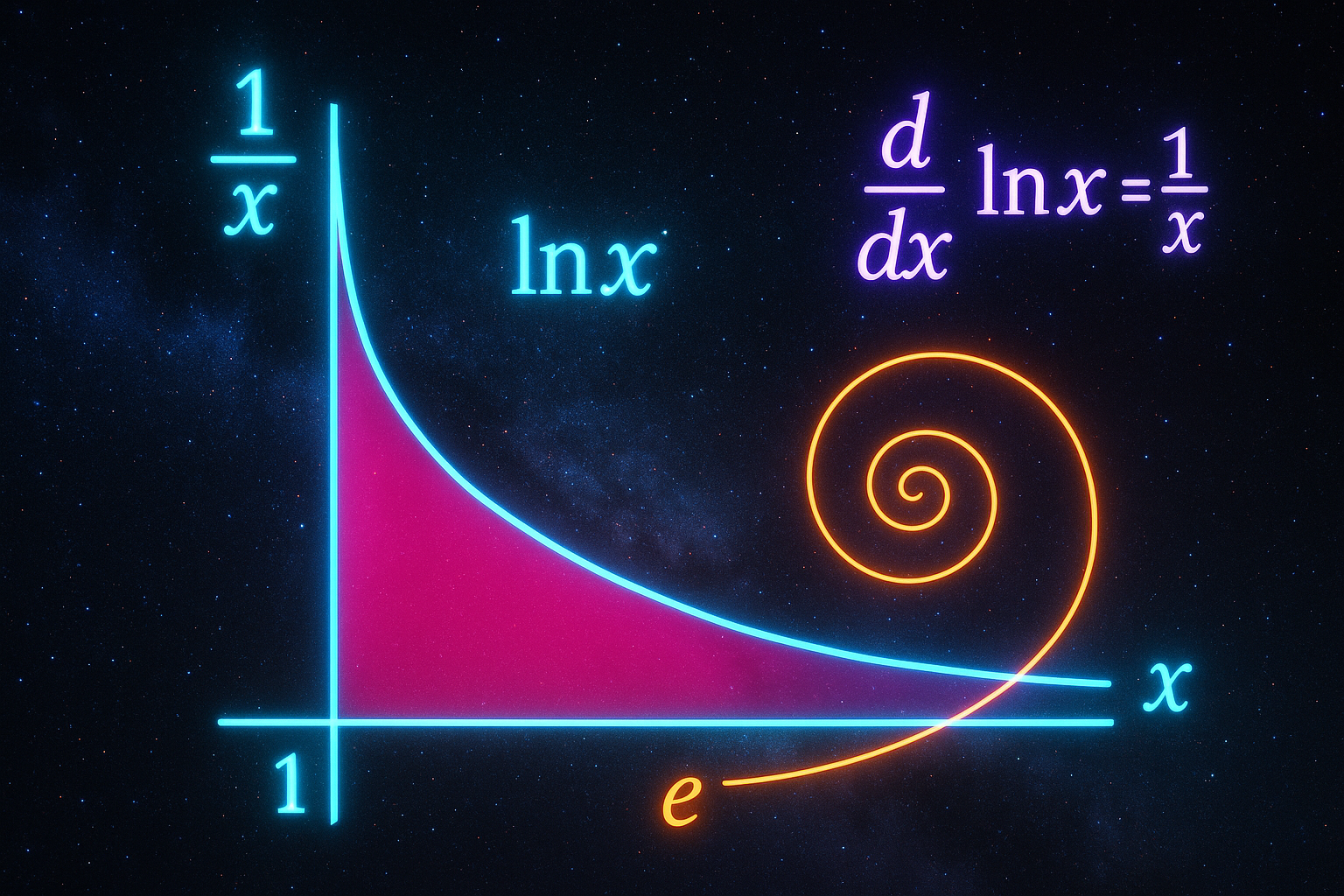
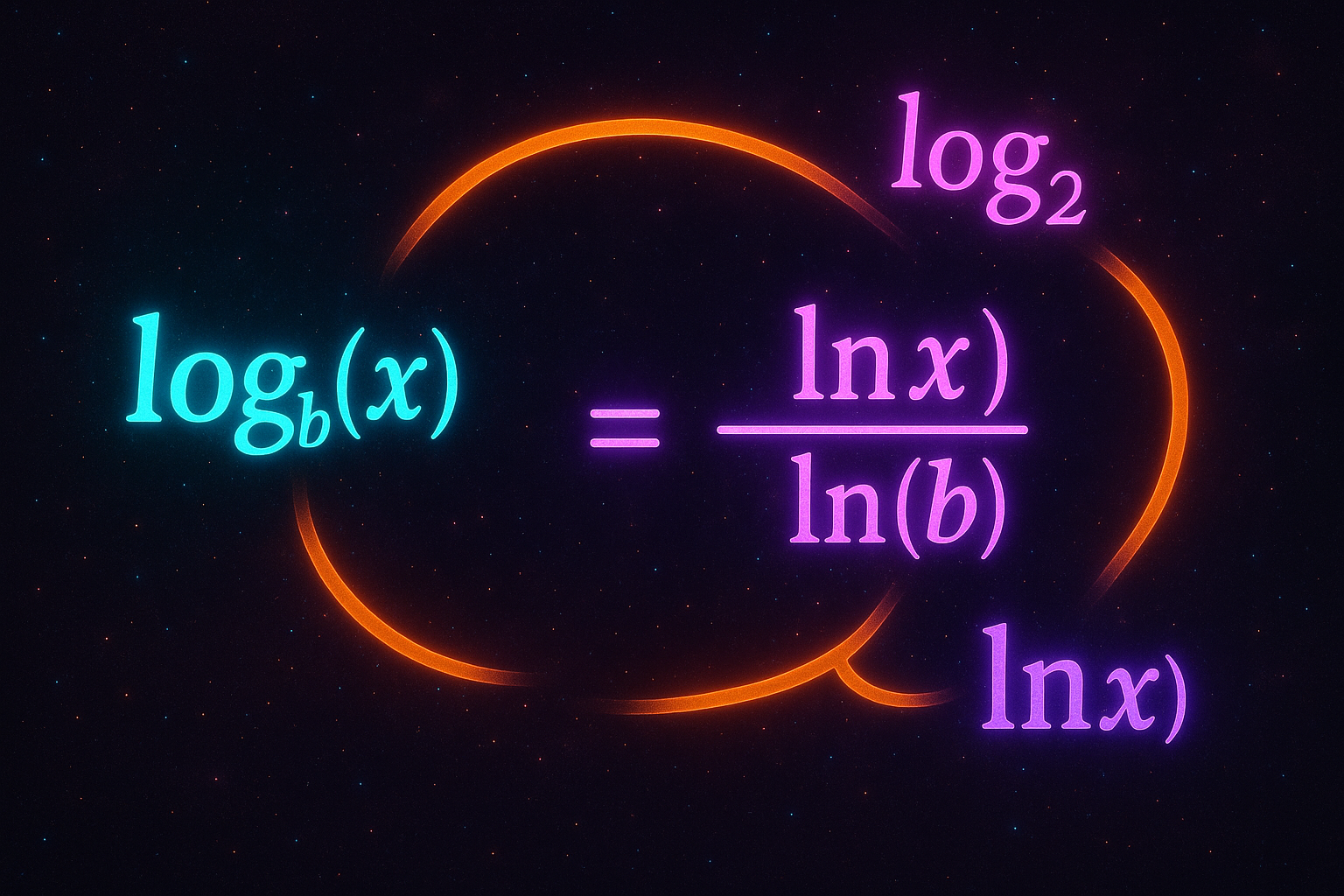


Comments ()