The Number e: The Base That Calculus Prefers
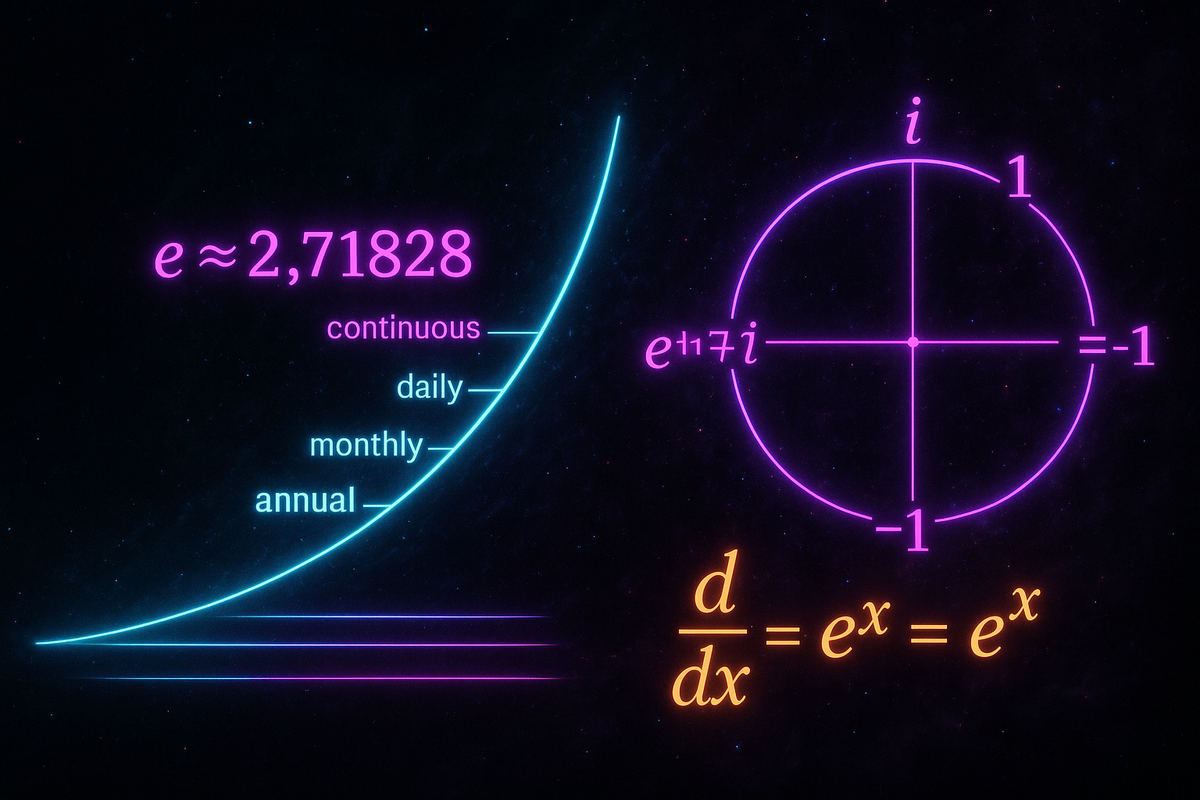
e ≈ 2.71828... is what you get when compound interest compounds forever.
Take $1, earn 100% interest for a year. If it compounds once, you get $2. If it compounds twice (50% each half-year), you get $2.25. Compound more often—monthly, daily, every second—and the amount approaches a limit.
That limit is e dollars.
e isn't constructed by mathematicians to be convenient. It emerges from the nature of continuous growth. It's the number that continuous compounding naturally produces.
Where e Comes From
Start with this limit:
e = lim(n→∞) (1 + 1/n)ⁿ
Try some values:
- n = 1: (1 + 1)¹ = 2
- n = 2: (1 + 1/2)² = 2.25
- n = 10: (1 + 0.1)¹⁰ ≈ 2.594
- n = 100: (1 + 0.01)¹⁰⁰ ≈ 2.705
- n = 1000: (1 + 0.001)¹⁰⁰⁰ ≈ 2.717
- n = ∞: e ≈ 2.71828182845...
The number converges. As compounding becomes continuous, the growth factor approaches e.
Why e Is Special
Many constants are defined by convenience. π is the ratio of circumference to diameter. √2 is the diagonal of a unit square.
e is different. It emerges from the deepest properties of growth and change:
Property 1: The derivative of eˣ is eˣ
d/dx(eˣ) = eˣ
This is unique. No other function equals its own derivative (except trivial multiples). The function eˣ is the fixed point of differentiation.
Property 2: The integral of eˣ is eˣ
∫eˣ dx = eˣ + C
Again unique. eˣ is unchanged by the fundamental operations of calculus.
Property 3: The series for e
e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + ...
= 1 + 1 + 0.5 + 0.167 + 0.042 + 0.008 + ...
This series converges rapidly. Use 10 terms and you get e to 7 decimal places.
e in Compound Interest
The compound interest formula with n compounding periods per year:
A = P(1 + r/n)ⁿᵗ
As n → ∞ (continuous compounding):
A = Pe^(rt)
This is the natural form. Continuous growth at rate r multiplies by e^r per unit time.
Example: $1000 at 5% for 10 years, compounded continuously:
A = 1000 × e^(0.05 × 10) = 1000 × e^0.5 ≈ $1,649
Compare to annual compounding: 1000 × (1.05)¹⁰ ≈ $1,629
Continuous compounding gives slightly more. The difference is the "bonus" from infinitely frequent compounding.
The Natural Logarithm
The natural logarithm (ln) is the logarithm base e:
ln(x) = log_e(x)
ln(e) = 1, ln(1) = 0, ln(eˣ) = x.
Why "natural"? Because:
d/dx(ln x) = 1/x
∫(1/x) dx = ln|x| + C
The simplest antiderivative of 1/x uses base e. Any other base would introduce ugly constants.
e and Differential Equations
The equation for natural growth or decay is:
dy/dt = ky
Solution: y = y₀e^(kt)
This is the fundamental equation of change. Any process where the rate of change is proportional to the current value is exponential with base e.
- Population growth: dP/dt = rP → P = P₀e^(rt)
- Radioactive decay: dN/dt = -λN → N = N₀e^(-λt)
- Cooling: dT/dt = -k(T - Tₐ) → exponential approach to ambient
e isn't chosen for these applications. It arises inevitably.
Euler's Formula
The most famous equation in mathematics:
e^(iπ) + 1 = 0
This connects five fundamental constants: e, i, π, 1, and 0.
More generally, Euler's formula says:
e^(iθ) = cos(θ) + i·sin(θ)
Exponentiation of imaginary numbers produces rotation. The exponential function unifies trigonometry and complex numbers.
Computing e
Method 1: Compound interest limit
(1 + 1/n)ⁿ for large n. Slow convergence.
Method 2: Series
e = ∑(1/n!) for n = 0 to ∞. Fast convergence.
Method 3: Continued fraction
e = 2 + 1/(1 + 1/(2 + 1/(1 + 1/(1 + 1/(4 + ...)))))
The pattern in the denominators is: 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, ...
e Is Transcendental
Like π, e is:
- Irrational: cannot be expressed as a fraction
- Transcendental: not the root of any polynomial with integer coefficients
This was proven by Hermite in 1873. You cannot construct e with ruler and compass.
The decimal expansion of e never repeats and follows no pattern: 2.71828182845904523536028747135266249775724709369995...
Why Use Base e Instead of Base 10?
Base 10 is natural for humans (10 fingers). But base e is natural for calculus.
d/dx(10ˣ) = 10ˣ × ln(10) ≈ 2.303 × 10ˣ
That extra factor of ln(10) appears because 10 isn't the natural base.
d/dx(eˣ) = eˣ
No extra factors. Clean. This is why mathematicians and scientists prefer e.
For practical calculations, base 10 (or base 2 for computers) is fine. But for theoretical work—differential equations, complex analysis, probability—e is the only sensible choice.
e in Probability
The probability of no events in a Poisson process with rate λ over time t:
P(0 events) = e^(-λt)
The base rate of "nothing happens" is an exponential decay.
The limit of the binomial distribution as n → ∞ and p → 0 with np = λ:
(n choose k) × pᵏ × (1-p)^(n-k) → e^(-λ) × λᵏ/k!
e appears because Poisson processes are the limit of many rare events.
The Bell Curve
The normal distribution has e in its formula:
f(x) = (1/√(2π)) × e^(-x²/2)
The e^(-x²) term creates the characteristic bell shape. Its integral over all x equals √π—another deep connection.
Why e Matters
- It's the natural base for growth. Continuous compounding at rate r multiplies by e^r.
- It simplifies calculus. d/dx(eˣ) = eˣ eliminates constant factors.
- It unifies mathematics. Euler's formula connects exponentials, trigonometry, and complex numbers.
- It appears everywhere. Probability, statistics, physics, engineering—e is inescapable.
- It emerges naturally. e isn't imposed by convention. It arises from the structure of continuous change.
The number e is what continuous growth naturally produces. That's why calculus prefers it.
Part 4 of the Exponential Functions series.
Previous: Exponential Decay: Half-Lives and Cooling Next: Compound Interest: Exponential Growth in Finance
Comments ()