Probability Explained
Probability is the mathematics of what we don't know.
Not ignorance—structured uncertainty. The kind of not-knowing that still follows rules. The kind that lets you reason rigorously about dice, diseases, decisions, and data.
This series covers probability from foundations to the theorems that make statistics possible. We'll explore the rules for combining uncertain events, Bayes' theorem for updating beliefs, random variables and distributions, and the remarkable theorems—the Law of Large Numbers and Central Limit Theorem—that explain why statistics works.
What You'll Learn
Foundations: What probability actually means, the axioms that make it rigorous, and the basic rules for computing with uncertainty.
Conditional Probability and Bayes: How new information changes probabilities, and the theorem that underlies modern machine learning, medical testing, and rational belief updating.
Random Variables: The bridge from events to numbers—how to describe uncertain quantities mathematically.
Distributions: The patterns uncertainty takes—binomial, normal, exponential—and when each appears.
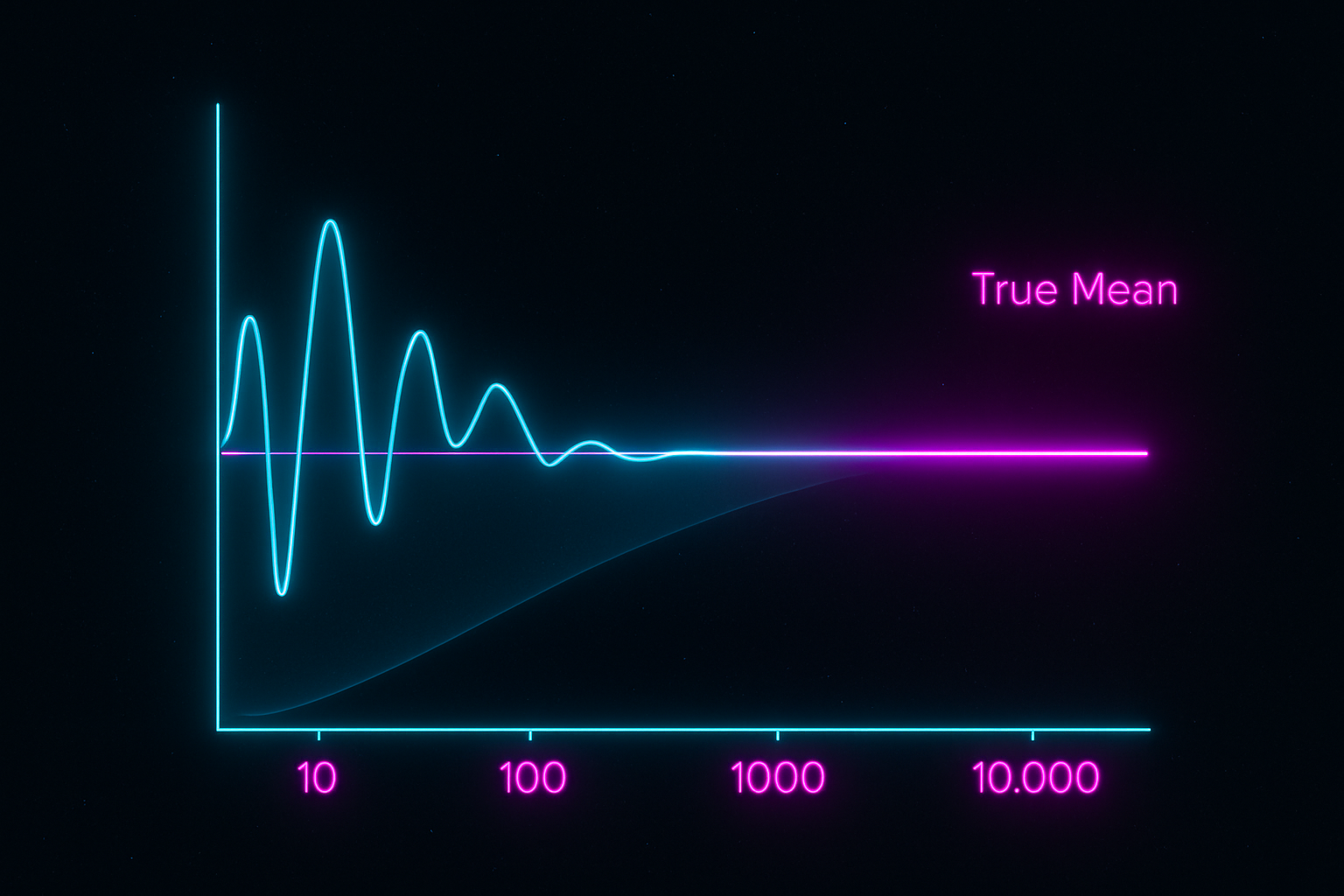
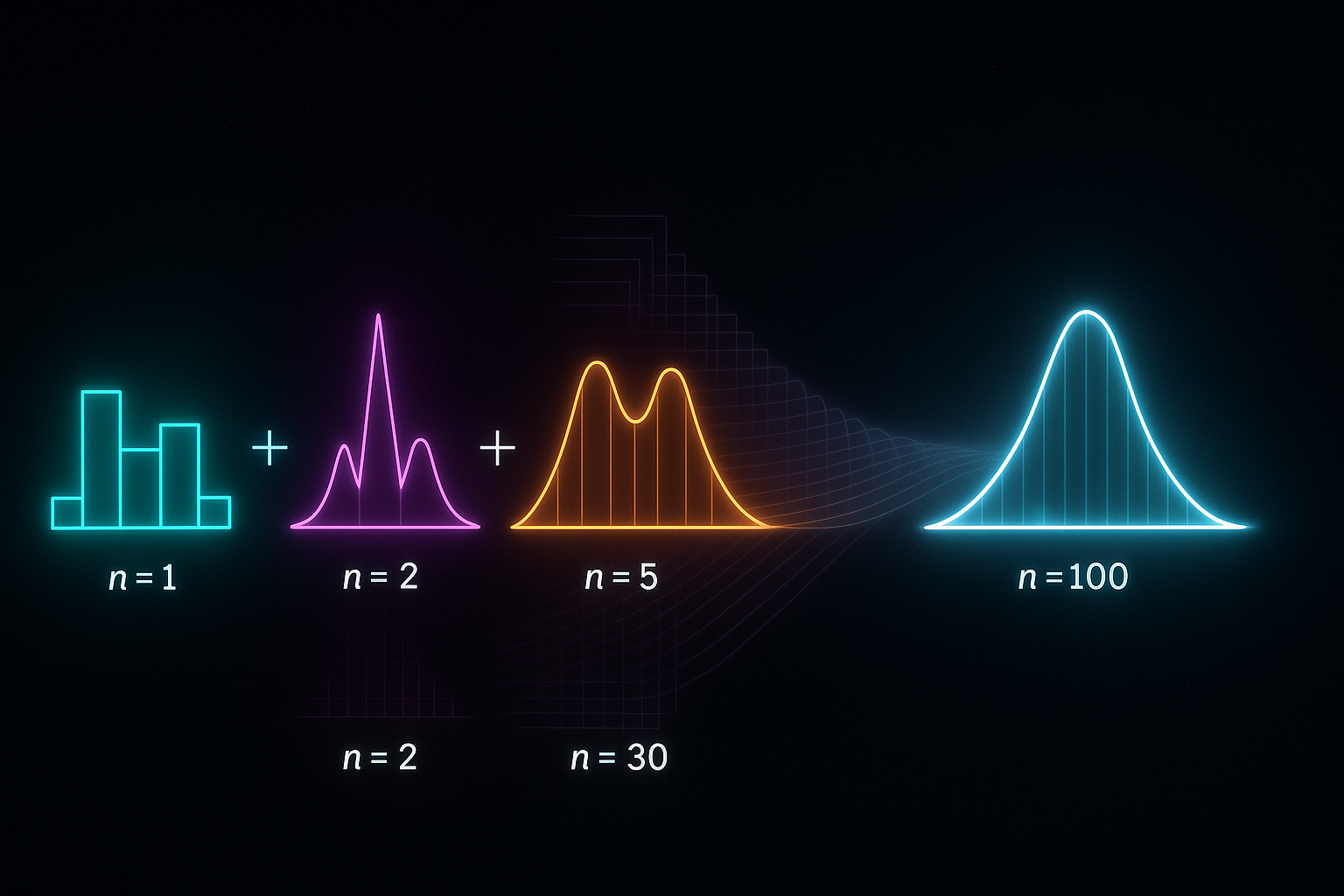
Limit Theorems: The deep results that explain why sampling works, why averages converge, and why the bell curve appears everywhere.
Why Probability Matters
Probability is the foundation of statistics, machine learning, quantum mechanics, and decision theory. Understanding it changes how you think about evidence, risk, prediction, and uncertainty itself.
Every claim about data—this drug works, this model predicts, this pattern is real—rests on probability. Master the mathematics and you see through the fog of uncertainty to what can actually be concluded.
This is the hub page for the Probability series. Start with "What Is Probability?" for the journey from frequentist coin flips to the mathematics that makes rational belief possible.
The Series


Comments ()