The Quadratic Formula: Why It Always Works

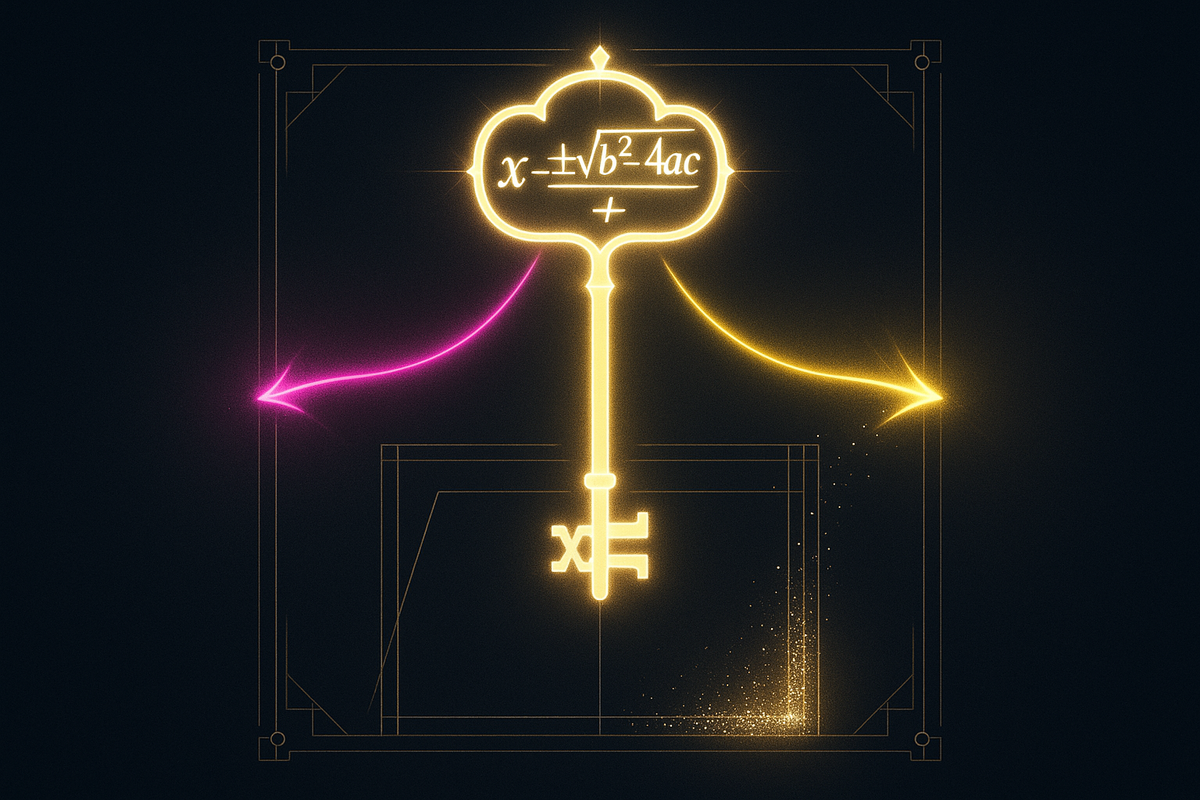
Solve once with letters, use forever with numbers.

That's the unlock. Someone solved ax² + bx + c = 0 using letters instead of specific numbers, and their answer became a formula you can use on any quadratic equation for the rest of your life. They did the work. You plug in values.

x = (-b ± √(b² - 4ac)) / 2a

This isn't a magic spell handed down from the math gods. It's what happens when you solve the general case — when you treat "any quadratic" as one problem instead of infinite separate problems. The quadratic formula is algebra's ultimate flex: do the hard work once, and every specific case becomes plug-and-chug.

Why You Can't Just Isolate x

With linear equations, you peel off operations until x stands alone. But quadratic equations have x² — and you can't just "undo" squaring when x appears in multiple terms.

3x + 5 = 17 → x = 4 (straightforward)

x² + 6x + 5 = 0 → ??? (x appears twice, in different powers)

The x² and the x are tangled together. You need a different approach.

Completing the Square: The Key Move

The trick is called completing the square. It transforms the messy quadratic into something you can take the square root of.

Here's the idea: x² + 6x + 9 is a perfect square. It equals (x + 3)².

x² + 6x + 9 = (x + 3)(x + 3) = (x + 3)²

Why does this help? Because (x + 3)² = something has a clear solution:

(x + 3)² = 16 x + 3 = ±4 x = -3 ± 4 x = 1 or x = -7

If you can rewrite a quadratic as (x + something)² = number, you can solve it.

How Completing the Square Works

Start with: x² + 6x + 5 = 0

Step 1: Move the constant. x² + 6x = -5

Step 2: Find the number that completes the square. Take half the coefficient of x, square it. Half of 6 is 3. Squared: 9.

Step 3: Add 9 to both sides. x² + 6x + 9 = -5 + 9 x² + 6x + 9 = 4

Step 4: Factor the left side. (x + 3)² = 4

Step 5: Take square roots of both sides. x + 3 = ±2

Step 6: Solve. x = -3 + 2 = -1, or x = -3 - 2 = -5

Check: (-1)² + 6(-1) + 5 = 1 - 6 + 5 = 0. ✓ Check: (-5)² + 6(-5) + 5 = 25 - 30 + 5 = 0. ✓

Deriving the Quadratic Formula

Now do the same thing, but with letters instead of numbers.

Start with: ax² + bx + c = 0

Step 1: Divide by a (get x² by itself). x² + (b/a)x + c/a = 0

Step 2: Move the constant. x² + (b/a)x = -c/a

Step 3: Complete the square. Half of b/a is b/2a. Squared: b²/4a². x² + (b/a)x + b²/4a² = -c/a + b²/4a²

Step 4: Factor the left side. (x + b/2a)² = -c/a + b²/4a²

Step 5: Simplify the right side (common denominator 4a²). (x + b/2a)² = (b² - 4ac)/4a²

Step 6: Take square roots. x + b/2a = ±√(b² - 4ac)/2a

Step 7: Solve for x. x = -b/2a ± √(b² - 4ac)/2a

x = (-b ± √(b² - 4ac)) / 2a

That's the quadratic formula. It came from completing the square on the general case.

What Each Part Means

x = (-b ± √(b² - 4ac)) / 2a

-b/2a: The axis of symmetry. Where the parabola peaks or bottoms out.

√(b² - 4ac): How far the solutions are from the axis. This is called the discriminant.

±: Quadratics generally have two solutions, one on each side of the axis.

The formula says: start at the axis of symmetry (-b/2a), then go left and right by the discriminant distance.

The Discriminant: How Many Solutions?

The expression under the square root, b² - 4ac, determines how many real solutions exist:

b² - 4ac > 0: Two distinct real solutions. The parabola crosses the x-axis twice.

b² - 4ac = 0: One real solution (a "repeated root"). The parabola touches the x-axis at one point.

b² - 4ac < 0: No real solutions. The parabola doesn't touch the x-axis. (The solutions are complex numbers.)

Before solving, you can calculate the discriminant to know what to expect.

Using the Formula

Example: Solve 2x² + 5x - 3 = 0

Identify: a = 2, b = 5, c = -3

Discriminant: b² - 4ac = 25 - 4(2)(-3) = 25 + 24 = 49

Since 49 > 0, two real solutions exist.

x = (-5 ± √49) / (2 × 2) x = (-5 ± 7) / 4

x = (-5 + 7)/4 = 2/4 = 1/2 x = (-5 - 7)/4 = -12/4 = -3

Solutions: x = 1/2 or x = -3

Check: 2(1/2)² + 5(1/2) - 3 = 1/2 + 5/2 - 3 = 3 - 3 = 0. ✓

Why It Always Works

The quadratic formula works because completing the square always works. It's a mechanical procedure that transforms any quadratic into solvable form.

No guessing. No luck. No special cases.

Give me any a, b, c (with a ≠ 0), and I can find x. The formula handles everything — nice integer solutions, ugly fractions, irrational numbers, even complex numbers.

Graphical Interpretation

A quadratic equation ax² + bx + c = 0 asks: where does the parabola y = ax² + bx + c cross the x-axis?

The solutions are the x-intercepts (or "roots" or "zeros") of the parabola.

• Two solutions: parabola crosses twice
• One solution: parabola touches once (vertex on x-axis)
• No real solutions: parabola doesn't reach the x-axis

The discriminant tells you whether the parabola makes it down (or up) to the x-axis.

Comparison: Factoring vs. Formula

Factoring works when the solutions are nice numbers: x² + 5x + 6 = 0 → (x + 2)(x + 3) = 0 → x = -2 or x = -3

Quadratic formula works always: x² + 5x + 6 = 0 → x = (-5 ± √(25-24))/2 = (-5 ± 1)/2 → x = -2 or x = -3

Same answer, different paths. Factoring is faster when it works. The formula is reliable when factoring fails or isn't obvious.

The ± Symbol

The ± means "plus or minus" — you get two equations in one:

x = (-b + √(b² - 4ac)) / 2a x = (-b - √(b² - 4ac)) / 2a

Quadratics can have two solutions because a parabola can cross a horizontal line twice. The ± captures both crossings.

Historical Note

People solved quadratic equations for thousands of years before the formula existed. Babylonians used geometric methods. Indian and Persian mathematicians developed algorithmic approaches.

The formula as we know it emerged when symbolic algebra matured — when mathematicians could write general expressions with letters and manipulate them.

The formula is a compression of an infinite number of specific solutions into one statement.

The Core Insight

The quadratic formula is completing the square, done once for all time.

It's not a magic spell. It's algebra solving the general case, so you don't have to repeat the work for each specific equation.

Plug in your a, b, c. The formula handles the rest. It will always give you the answer — whether that answer is nice integers, messy fractions, irrational roots, or complex numbers.

Every quadratic has exactly two solutions (counting multiplicity and complex numbers). The formula finds them.

Part 4 of the Algebra Fundamentals series.

Previous: Solving Linear Equations: Isolating the Unknown Next: Factoring Quadratics: Finding the Numbers That Multiply and Add