Sequences and Series Explained

A sequence is a list with a rule. A series is what you get when you add it up.
That's it. Everything else—convergence, summation notation, infinite sums—is just the question of what happens when you follow a pattern and keep adding.
What You'll Learn
This series covers the mathematics of ordered patterns and their sums:
- What Are Sequences and Series? — The difference between listing and summing
- Arithmetic Sequences — When you add the same amount each time
- Geometric Sequences — When you multiply by the same factor each time
- The Fibonacci Sequence — When each term depends on the previous two
- Sigma Notation — The shorthand for writing sums
- Arithmetic Series — Summing arithmetic sequences
- Geometric Series — Summing geometric sequences
- Infinite Series — When sums never stop but still converge
- Convergence Tests — How to tell if an infinite series has a finite sum
- Power Series — Polynomials that go on forever
- Recursion — Sequences defined by their own terms
- Synthesis — Sequences and series as the language of patterns
Prerequisites
- Algebra fundamentals (variables, expressions, basic equations)
- Exponents and powers
- Comfort with fractions and negative numbers
Why This Matters
Sequences and series are how mathematics captures patterns that grow, accumulate, and converge. They're the foundation for:
- Calculus — Taylor series approximate functions as infinite polynomials
- Finance — Compound interest and annuities are geometric series
- Computer science — Algorithm analysis uses recurrence relations
- Physics — Fourier series decompose signals into waves
When you understand sequences and series, you understand how finite rules generate infinite patterns—and how infinite processes can have finite results.
This is the hub page for the Sequences Series series.
Next: What Are Sequences and Series? Ordered Numbers and Their Sums
The Series
What Are Sequences and Series? Ordered Numbers and Their Sums
Sequences are ordered lists - series are sums of sequences - infinite patterns from finite rules

Arithmetic Sequences: Adding the Same Amount Each Time
Arithmetic sequences have constant differences - 2 5 8 11 adds 3 each time

Geometric Sequences: Multiplying by the Same Factor
Geometric sequences have constant ratios - 2 6 18 54 multiplies by 3 each time

The Fibonacci Sequence: When Each Term Is the Sum of the Previous Two
Fibonacci numbers appear in nature art and mathematics - 1 1 2 3 5 8 13 and beyond

Sigma Notation: Writing Sums Compactly
Sigma notation compresses long sums into short expressions - Σ tells you what to add and where
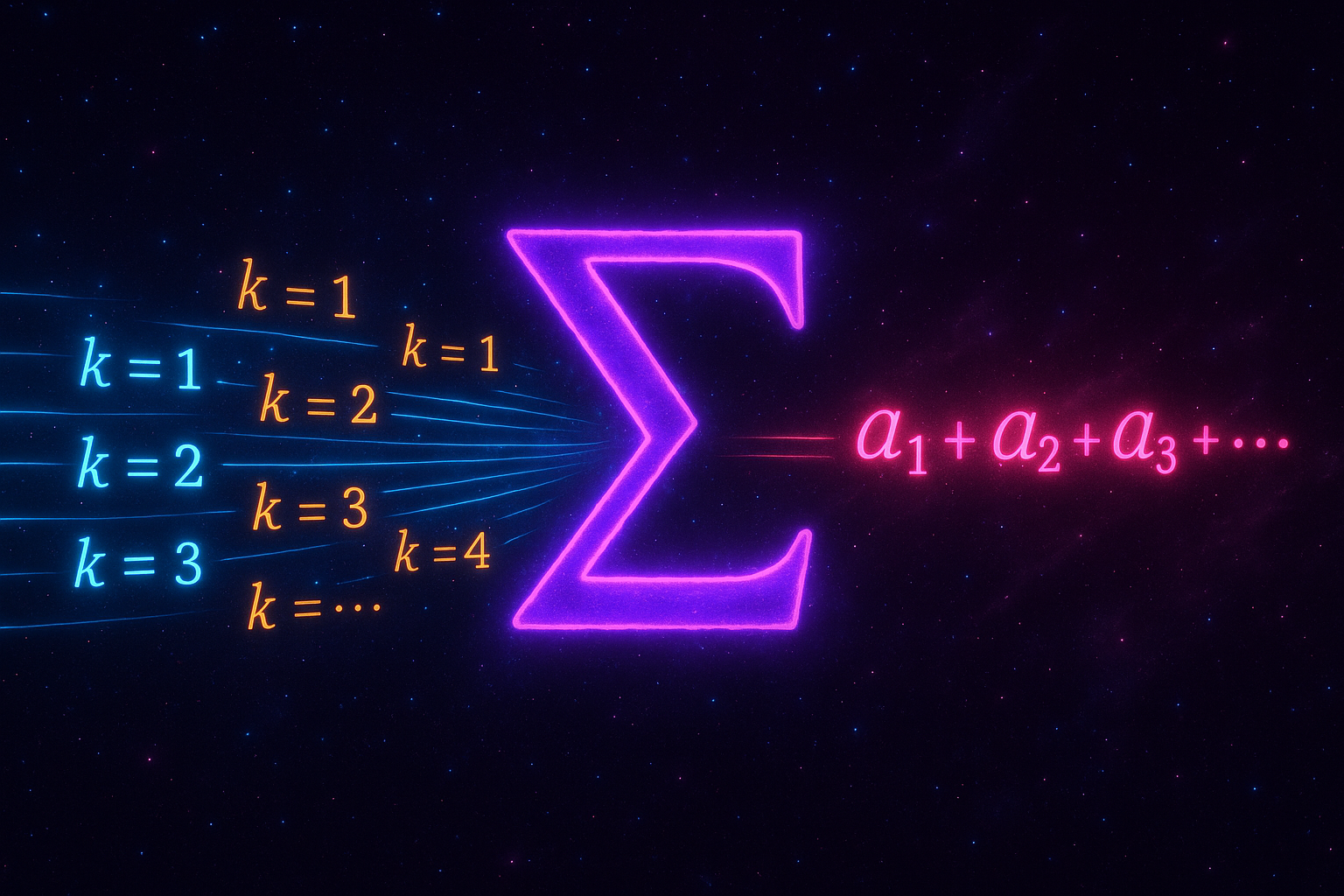
Arithmetic Series: Summing Arithmetic Sequences
Arithmetic series have a formula - n terms times first plus last divided by two

Geometric Series: Summing Geometric Sequences
Geometric series have a beautiful formula - a(1-r^n)/(1-r) captures the pattern
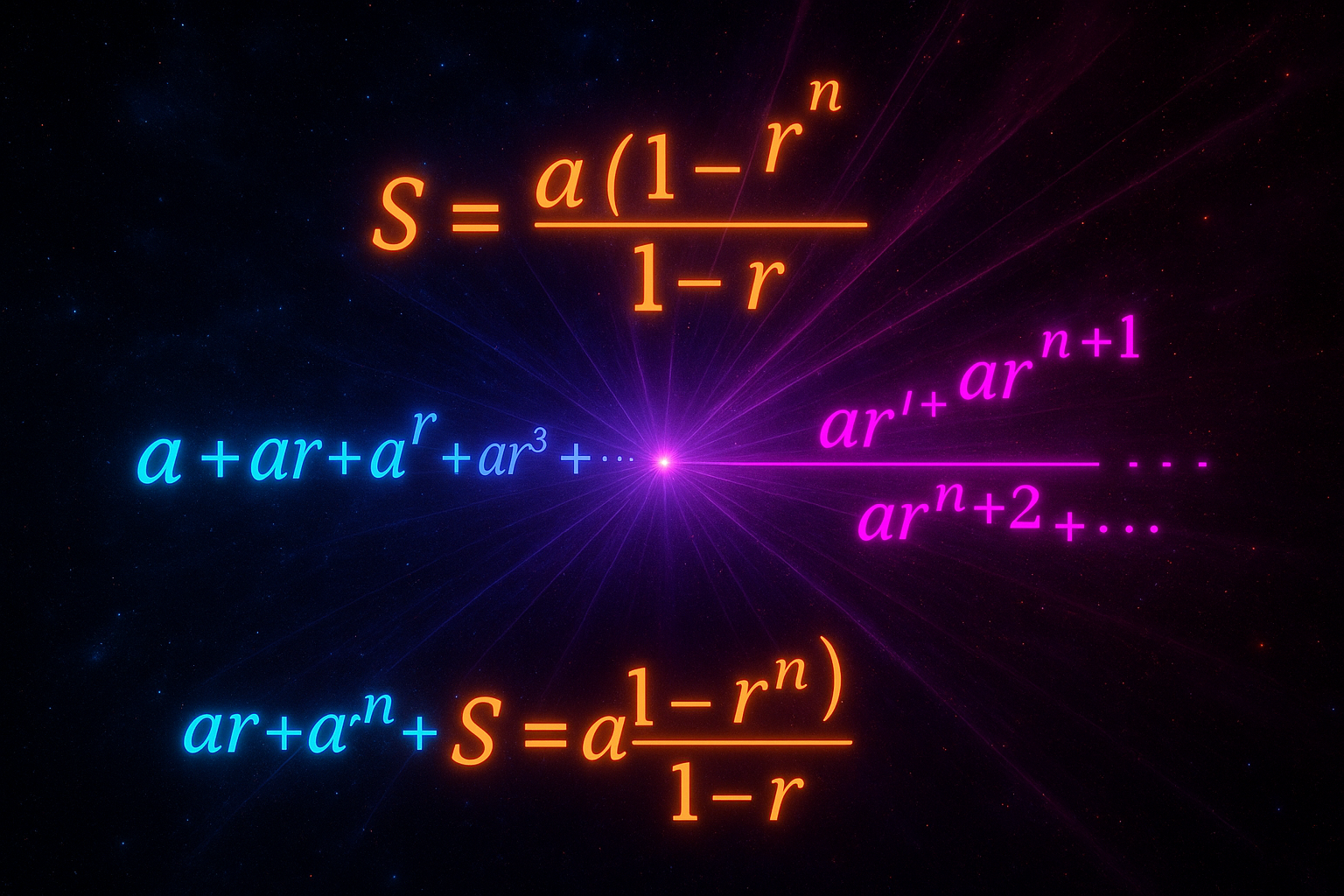
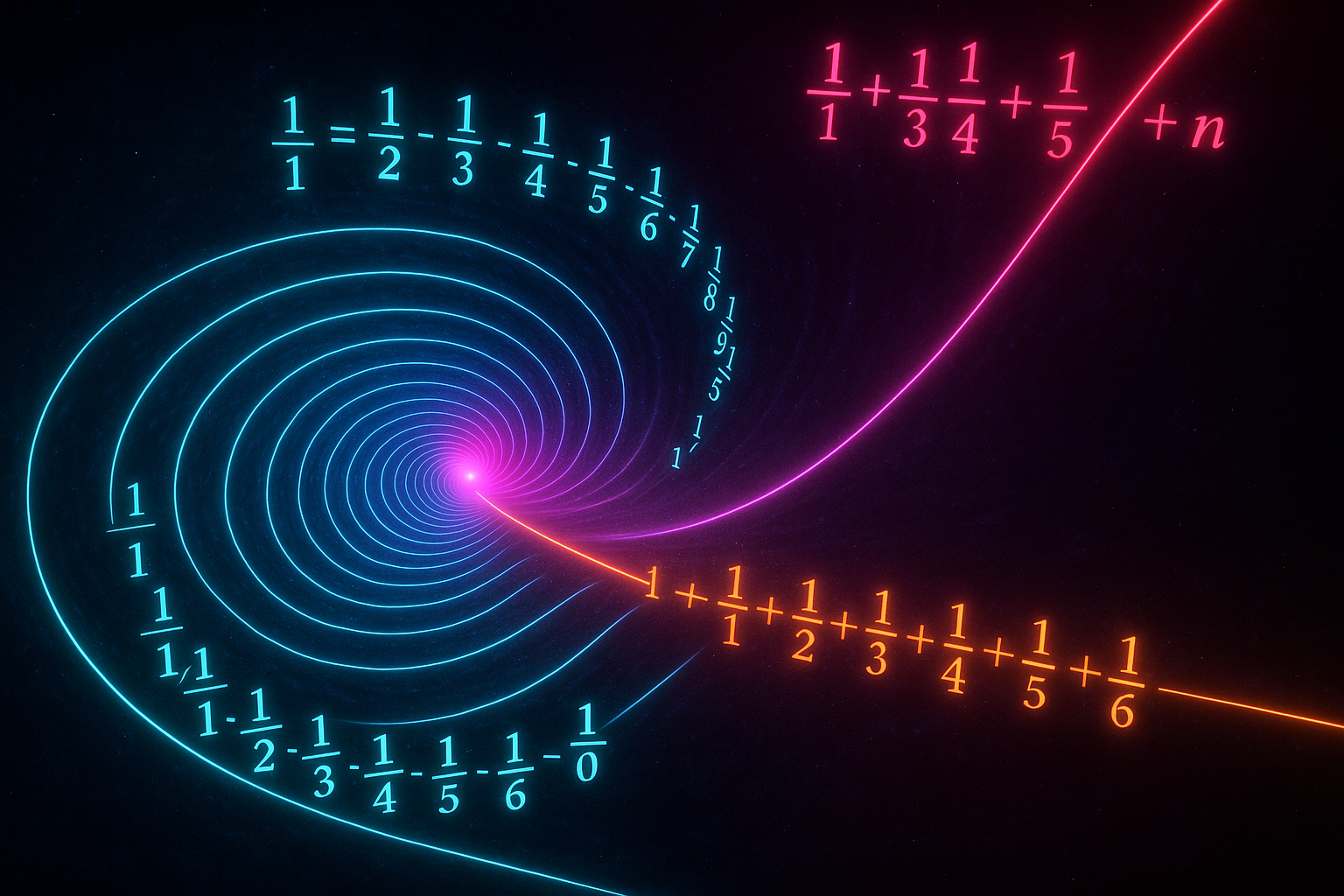
Infinite Series: When Sums Never Stop but Still Converge
Infinite series can have finite sums - 1/2 + 1/4 + 1/8 + ... equals 1
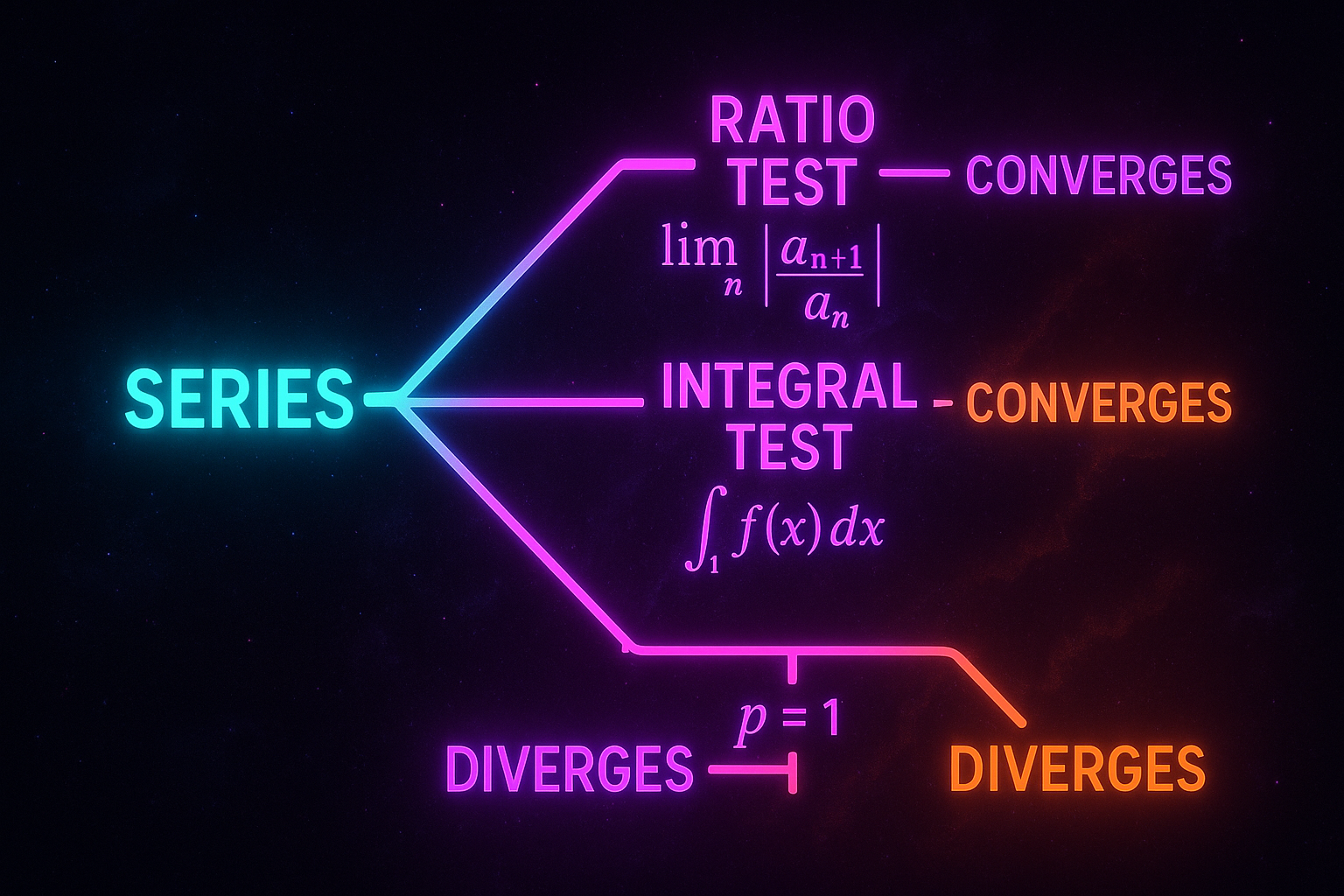
Convergence Tests: When Does an Infinite Series Have a Sum?
Convergence tests determine if infinite series sum to a finite value - ratio test comparison test
Power Series: Polynomials That Go On Forever
Power series represent functions as infinite polynomials - Taylor and Maclaurin series
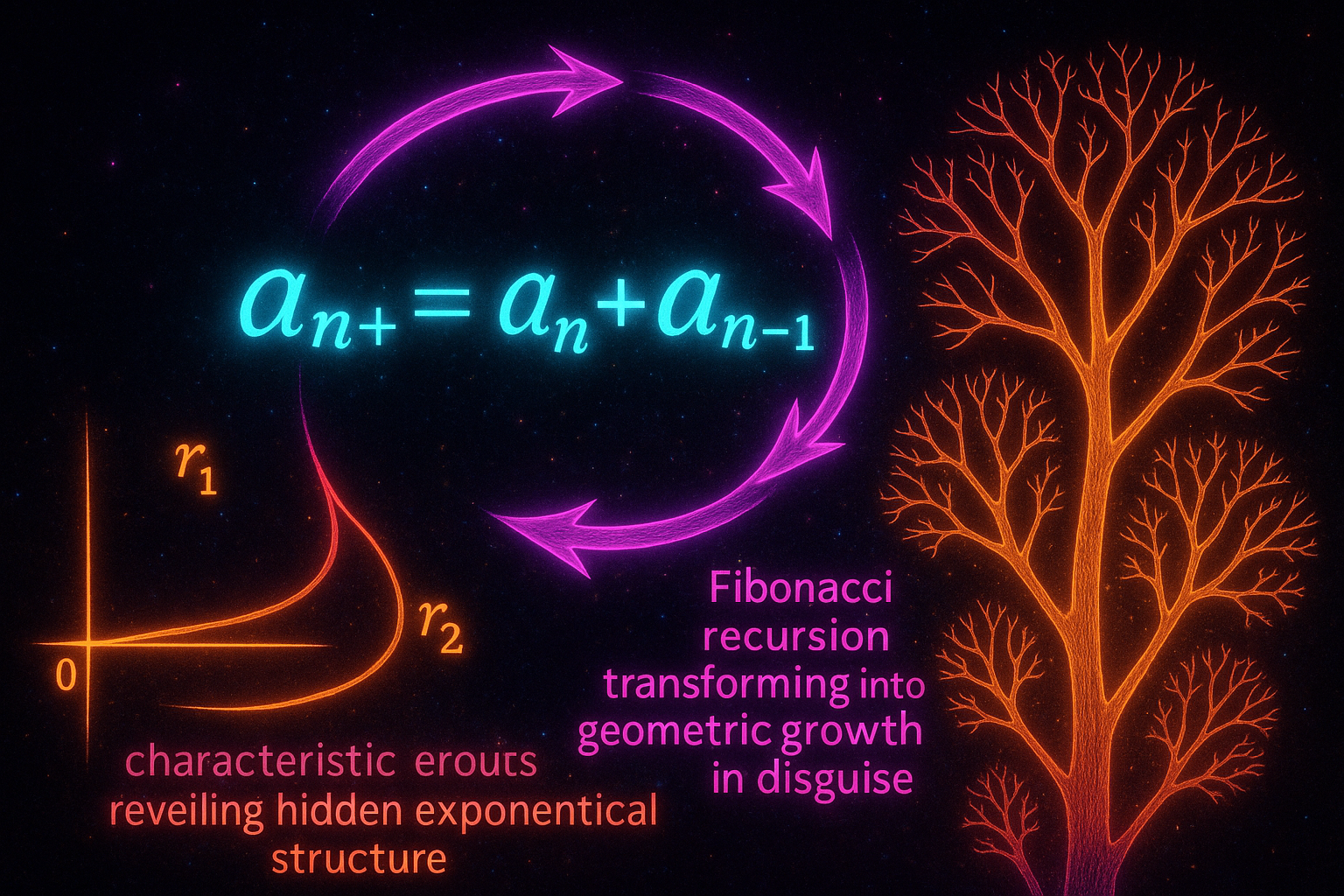
Recursion: Sequences Defined by Their Own Terms
Recursive sequences define each term using previous terms - the pattern contains itself
Synthesis: Sequences and Series as the Language of Patterns
Sequences and series capture how quantities grow accumulate and converge

Comments ()