Spontaneous Reactions: When ΔG Goes Negative

The word "spontaneous" misleads everyone.

In everyday language, spontaneous means sudden, impulsive, happening immediately. A spontaneous decision. A spontaneous combustion.

In thermodynamics, spontaneous means something precise and different: thermodynamically favorable. A spontaneous reaction is one where ΔG < 0. That's it. No claim about speed, no requirement for immediacy.

Diamonds transforming to graphite is spontaneous (ΔG < 0). It takes billions of years.

What Spontaneous Actually Means

A spontaneous process is one that: 1. Can occur without continuous external energy input 2. Increases the total entropy of the universe 3. Has negative Gibbs free energy change (at constant T, P)

These three statements are equivalent. They all say the same thing in different thermodynamic languages.

The pebble: "Spontaneous" is physics jargon for "thermodynamically downhill." It says nothing about speed, nothing about whether it will actually happen in your lifetime.

Spontaneous ≠ Fast

This is the most common confusion. Let's kill it.

Fast but non-spontaneous: - Electrolysis (splitting water with electricity): Happens quickly but requires continuous energy input. ΔG > 0.

Slow but spontaneous: - Diamond to graphite: ΔG ≈ -3 kJ/mol. Spontaneous. Rate is essentially zero at room temperature. - Iron rusting: ΔG << 0. Spontaneous. Takes months to years depending on conditions.

Fast and spontaneous: - Combustion of gasoline: ΔG << 0, and fast once initiated. - Acid-base neutralization: ΔG < 0, nearly instantaneous.

The difference is kinetics. ΔG tells you thermodynamics—where the system wants to go. Activation energy tells you kinetics—how hard it is to get there.

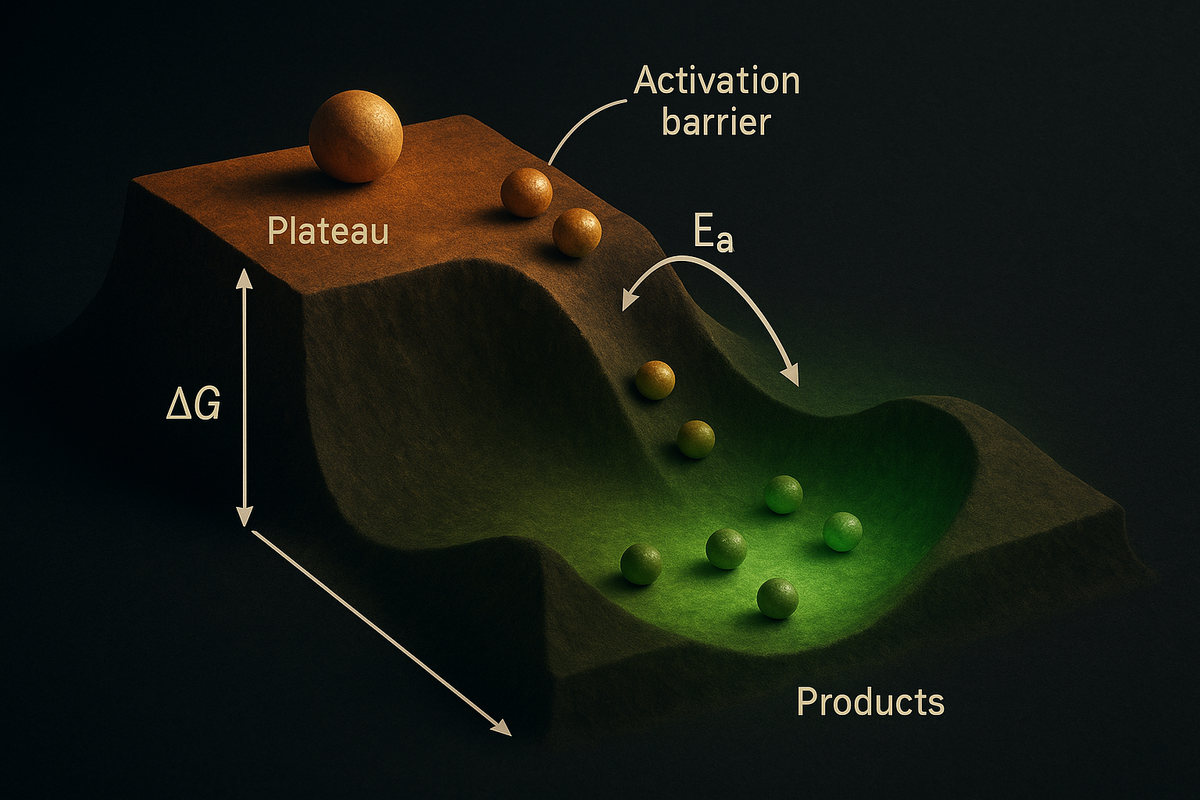
The Activation Energy Barrier

Even when ΔG < 0, reactions may not proceed because of an activation energy barrier.

Imagine a ball on a hill. It wants to roll down (ΔG < 0). But there's a ridge between it and the valley. The ball must first go up and over the ridge before rolling down.

The ridge height is the activation energy (Ea). If Ea is high, even thermodynamically favorable reactions are slow.

How to speed up spontaneous reactions: - Add heat (more molecules have energy to cross the barrier) - Add catalyst (lowers the barrier without changing ΔG) - Increase concentration (more collision opportunities)

The pebble: ΔG determines the destination. Ea determines when you arrive. Spontaneous reactions with high Ea may take geological time.

Spontaneity and Reversibility

Spontaneous (ΔG < 0): Forward reaction is favored.

Non-spontaneous (ΔG > 0): Reverse reaction is favored.

Reversible (ΔG ≈ 0): Both directions are thermodynamically similar. Small changes flip the favored direction.

Near equilibrium, reactions are reversible. Far from equilibrium, they're effectively one-way.

ATP hydrolysis (ΔG ≈ -30 kJ/mol) is essentially irreversible under cellular conditions. You can't easily un-hydrolyze ATP without coupling to another favorable reaction.

The Four Cases Revisited

From ΔG = ΔH - TΔS:

Case 1: ΔH < 0, ΔS > 0 Exothermic and entropy-increasing. Both terms favor spontaneity. ΔG < 0 at all temperatures. Always spontaneous. Example: Combustion of hydrocarbons.

Case 2: ΔH > 0, ΔS < 0 Endothermic and entropy-decreasing. Both terms oppose spontaneity. ΔG > 0 at all temperatures. Never spontaneous. Example: Concentrating a dilute gas (doesn't happen on its own).

Case 3: ΔH < 0, ΔS < 0 Exothermic but entropy-decreasing. Enthalpy favors, entropy opposes. ΔG < 0 at low T, ΔG > 0 at high T. Spontaneous when cold. Example: Freezing water.

Case 4: ΔH > 0, ΔS > 0 Endothermic but entropy-increasing. Enthalpy opposes, entropy favors. ΔG > 0 at low T, ΔG < 0 at high T. Spontaneous when hot. Example: Melting ice, dissolving ammonium nitrate.

Spontaneity in Biology

Cells are spontaneity managers.

Most cellular work is non-spontaneous: protein synthesis, DNA replication, maintaining ion gradients, muscle contraction. These all have ΔG > 0.

How do cells make non-spontaneous things happen? Coupling.

By linking an unfavorable reaction to a favorable one, the combined ΔG can be negative. ATP hydrolysis (ΔG ≈ -30.5 kJ/mol) is the universal coupler.

Example: Glutamine synthesis - Glutamate + NH₃ → Glutamine: ΔG = +14 kJ/mol (non-spontaneous) - ATP → ADP + Pi: ΔG = -30.5 kJ/mol (spontaneous) - Coupled: ΔG = +14 - 30.5 = -16.5 kJ/mol (spontaneous)

The favorable reaction pays the thermodynamic cost of the unfavorable one.

The pebble: Life is a network of coupled reactions. Non-spontaneous processes are dragged along by spontaneous ones. The accounting always balances—total ΔG is always negative.

Spontaneity and Equilibrium

Spontaneous reactions don't run forever. They proceed until equilibrium (ΔG = 0).

At equilibrium: - ΔG = 0 - Q = K - No net change (forward rate = reverse rate)

A reaction with large negative ΔG° has equilibrium far toward products. A reaction with large positive ΔG° has equilibrium far toward reactants.

But equilibrium is always reached eventually—every spontaneous reaction burns out its free energy gradient.

Le Chatelier's Principle

When a system at equilibrium is disturbed, it shifts to counteract the disturbance. This is Le Chatelier's principle.

From the ΔG perspective: - Adding reactants: Q decreases, ΔG becomes more negative, reaction shifts right - Adding products: Q increases, ΔG becomes more positive, reaction shifts left - Raising temperature: Depends on sign of ΔH - Increasing pressure: Depends on moles of gas

Le Chatelier is just ΔG seeking zero. Disturb the balance, and the system responds by moving toward the new equilibrium.

Spontaneous Reactions in Industry

Industrial chemistry is applied spontaneity.

Ammonia synthesis (Haber process): N₂ + 3H₂ ⇌ 2NH₃, ΔG° = -33 kJ/mol

Spontaneous, but slow at low temperature (kinetics) and unfavorable at high temperature (entropy opposes, since moles of gas decrease). Solution: intermediate temperature + catalyst + high pressure.

Sulfuric acid production: Multiple steps, all managed for optimal ΔG and rate. Heat recovery from exothermic steps powers endothermic ones.

Petroleum refining: Cracking (breaking large molecules) is entropy-favored but requires heat. Reforming (rearranging structures) is carefully controlled for optimal ΔG.

Industry doesn't fight thermodynamics—it works with it, optimizing conditions where ΔG and kinetics align.

Spontaneity and the Second Law

The Second Law says entropy of the universe increases. How does this connect to ΔG < 0?

For a spontaneous process at constant T, P:

ΔS_universe = ΔS_system + ΔS_surroundings ΔS_surroundings = -ΔH_system / T (heat released to surroundings)

ΔS_universe = ΔS_system - ΔH_system / T

Multiply by -T:

-TΔS_universe = ΔH_system - TΔS_system = ΔG

Second Law requires ΔS_universe ≥ 0, so ΔG ≤ 0.

The pebble: ΔG < 0 is the Second Law wearing a chemistry costume. Spontaneity is entropy increase, translated for constant T and P.

Exceptions and Edge Cases

Metastable states: A system can be stuck in a local minimum, even though a lower minimum exists elsewhere. Diamond is metastable—it sits in a local minimum even though graphite's minimum is lower. The barrier between them is too high.

Driven systems: With continuous energy input, you can maintain non-spontaneous conditions indefinitely. Living cells are driven systems, kept far from equilibrium by ATP-burning metabolism.

Fluctuations: At molecular scales, spontaneous entropy decreases occur briefly. A few molecules might cluster against the gradient. But statistical mechanics says these fluctuations are rare and short-lived.

Summary: The Spontaneity Checklist

A reaction is spontaneous if: - ΔG < 0 (definition) - Products are lower in free energy than reactants - Universe's entropy increases as a result - It can proceed without continuous energy input

A reaction being spontaneous does NOT mean: - It happens fast - It happens at all (activation barrier may prevent it) - It goes to completion (equilibrium is the endpoint) - It's irreversible (depends on magnitude of ΔG)

Further Reading

- Atkins, P. & de Paula, J. (2014). Physical Chemistry. Oxford University Press. - Dill, K. & Bromberg, S. (2011). Molecular Driving Forces. Garland Science.

This is Part 4 of the Gibbs Free Energy series. Next: "Temperature's Hidden Power: The Gibbs-Helmholtz Equation"