Trees: Connected Graphs Without Cycles

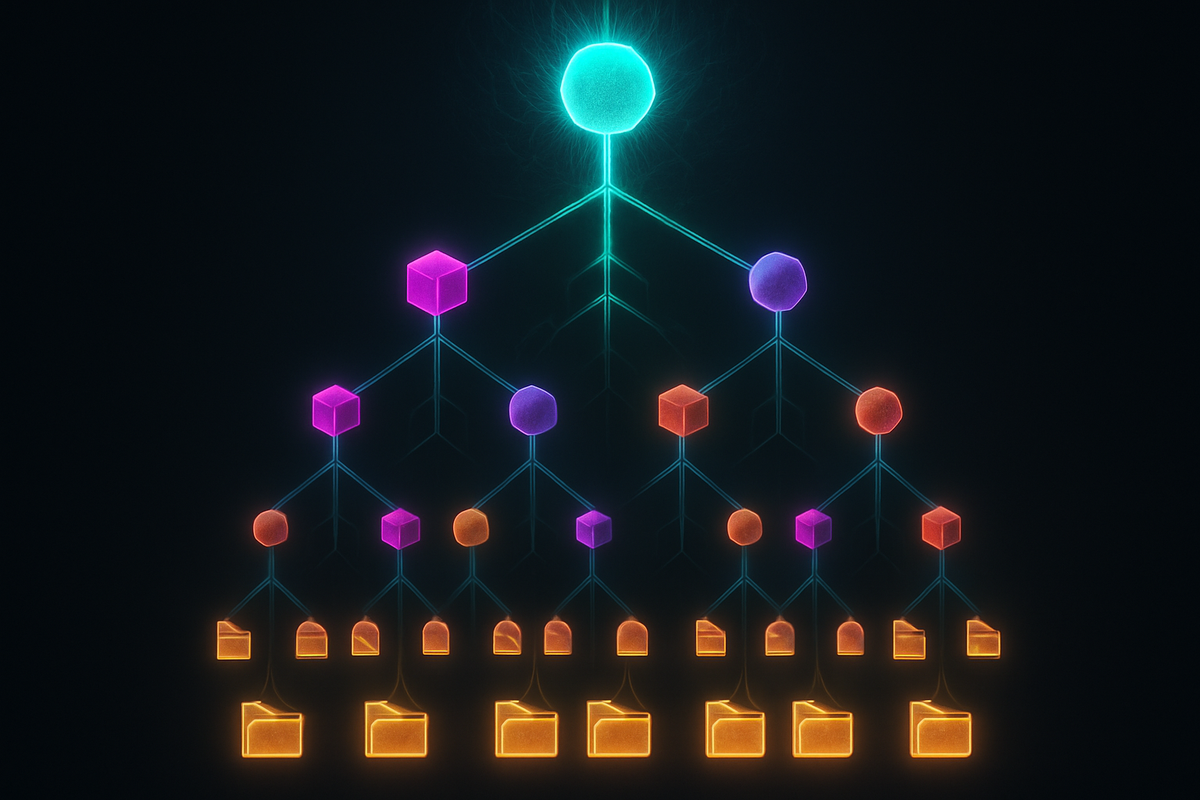
A tree is a graph with one iron rule: no cycles.

Start at any node. Walk along edges. You can reach every other node, but you can never return to where you started without backtracking. There's exactly one path between any two nodes—no shortcuts, no loops, no redundancy.

This constraint—connected but acyclic—creates a structure so fundamental that it appears everywhere:

• File systems: Folders contain subfolders, forming a tree from root directory down
• Family trees: Parents to children, ancestry branching through generations
• Corporate hierarchies: CEO to VPs to managers to employees
• Decision processes: Choose A or B, then C or D, branching possibilities
• Evolutionary trees: Species diverging from common ancestors
• Neural networks: Hierarchical feature extraction from input to output
• Parse trees: How compilers understand code syntax
• Binary search trees: How databases and search algorithms organize data

Trees aren't just a special kind of graph. They're the skeleton of hierarchical structure itself.

The Definition

A tree is a connected, acyclic graph.

Equivalent definitions:

• A connected graph with n nodes has exactly n-1 edges
• A graph where there's exactly one path between any two nodes
• A connected graph where removing any edge disconnects it
• An acyclic graph where adding any edge creates a cycle

These definitions are mathematically equivalent. Pick whichever makes the problem clearest.

Key properties:

• n nodes, n-1 edges
• Connected (one component)
• No cycles
• Unique paths between nodes

Rooted Trees: Hierarchy Emerges

A rooted tree designates one node as the root. All other nodes have a parent-child relationship defined by distance from the root.

Terminology:

• Root: The top node (no parent)
• Parent: A node's direct predecessor toward the root
• Child: A node's direct successor away from the root
• Leaf: A node with no children (terminal node)
• Internal node: A node with at least one child
• Siblings: Nodes sharing the same parent
• Ancestor: Any node on the path from a given node to the root
• Descendant: Any node reachable going away from the root
• Subtree: A node and all its descendants
• Depth of a node: Distance from root
• Height of a tree: Maximum depth (longest root-to-leaf path)
• Level: All nodes at the same depth

Rooted trees encode hierarchy. The root is the origin; leaves are endpoints. Every node has a unique path to the root.

Binary Trees: Two Children Max

A binary tree is a rooted tree where each node has at most two children: left and right.

Binary trees are the workhorse of computer science.

Types:

• Full binary tree: Every node has 0 or 2 children (no nodes with only 1 child)
• Complete binary tree: All levels filled except possibly the last, which fills left-to-right
• Perfect binary tree: All internal nodes have 2 children, all leaves at the same depth (2^h nodes at height h)
• Balanced binary tree: Left and right subtrees of any node differ in height by at most 1

Why binary? Computers are binary machines. Decisions split two ways (true/false, left/right, 0/1). Binary trees match computational logic.

Binary Search Trees: Sorted Data

A binary search tree (BST) is a binary tree where:

• Left subtree contains values < node
• Right subtree contains values > node

This ordering enables O(log n) search (in balanced trees).

Search algorithm:

1. Start at root
2. If target < current, go left; if target > current, go right
3. If target = current, found; if null, not in tree

Insertion: Follow search path to where the value should be, insert as leaf.

Deletion: More complex (three cases: leaf, one child, two children).

Problem: Unbalanced BSTs degrade to O(n) search (if insertions happen in sorted order, tree becomes a linked list).

Solution: Self-balancing BSTs.

AVL Trees

Maintain balance: heights of left/right subtrees differ by at most 1. Rotations restore balance after insertion/deletion. Guarantees O(log n) operations.

Red-Black Trees

Less strict balancing (faster insertions/deletions), still O(log n) guarantees. Used in many standard libraries (C++ std::map, Java TreeMap).

BSTs underlie databases, file systems, compilers—anywhere you need fast sorted data access.

Heaps: Priority Queues

A heap is a complete binary tree satisfying the heap property:

• Max-heap: Every parent ≥ its children (root is maximum)
• Min-heap: Every parent ≤ its children (root is minimum)

Heaps enable O(log n) insertion and O(log n) extraction of min/max element.

Implementation: Store heap as an array. For node at index i:

• Left child: 2i + 1
• Right child: 2i + 2
• Parent: (i - 1) / 2

No pointers needed—implicit tree structure via array indices.

Applications:

• Priority queues: Process highest/lowest priority task
• Heap sort: O(n log n) sorting algorithm
• Dijkstra's algorithm: Extract minimum-distance node efficiently
• Event-driven simulation: Process events in time order

Spanning Trees: Connecting All Nodes

A spanning tree of a graph is a subgraph that:

• Includes all nodes
• Is a tree (connected, acyclic)

If the original graph has n nodes, a spanning tree has n-1 edges.

Minimum Spanning Tree (MST)

For weighted graphs, the MST minimizes total edge weight.

Kruskal's Algorithm:

1. Sort edges by weight
2. Add edges one by one, skipping any that form cycles
3. Stop when you have n-1 edges

Prim's Algorithm:

1. Start from any node
2. Repeatedly add cheapest edge connecting tree to a new node
3. Stop when all nodes included

Both find MST in O(E log V) time.

Applications:

• Network design (minimize cable length)
• Clustering (MST-based clustering in machine learning)
• Image segmentation
• Approximation algorithms (e.g., TSP)

Tree Traversals: Visiting Every Node

How do you visit every node in a tree exactly once?

Depth-First Search (DFS)

Go deep before going wide.

Pre-order: Visit node, then left subtree, then right subtree. In-order: Visit left subtree, then node, then right subtree. (For BSTs, visits nodes in sorted order!) Post-order: Visit left subtree, then right subtree, then node.

Implementation: Use recursion or a stack.

Use cases:

• Pre-order: Copying a tree, serialization
• In-order: Getting sorted data from BST
• Post-order: Deleting a tree, evaluating expression trees

Breadth-First Search (BFS)

Visit level-by-level.

Implementation: Use a queue.

Use cases:

• Finding shortest path (unweighted graphs)
• Level-order traversal
• Serialization preserving structure

Traversal choice depends on the problem. DFS is recursive and natural. BFS is iterative and finds shortest paths.

Expression Trees: Parsing Math

An expression tree represents mathematical expressions:

• Leaves: Operands (numbers, variables)
• Internal nodes: Operators (+, -, ×, ÷)

Example: The expression (3 + 5) × (2 - 1)

      ×
     / \
    +   -
   / \ / \
  3  5 2  1

Evaluation: Post-order traversal.

1. Evaluate left subtree: 3 + 5 = 8
2. Evaluate right subtree: 2 - 1 = 1
3. Apply root operator: 8 × 1 = 8

Why trees? They encode precedence and associativity naturally. Compilers parse code into syntax trees for evaluation and optimization.

Tries: Prefix Trees for Strings

A trie (pronounced "try") is a tree for storing strings where each node represents a character.

Example: Store {"cat", "car", "dog"}

      root
      / \
     c   d
    / \   \
   a   o
  / \   \
 t   r   g

Shared prefixes share paths. Each path from root to leaf spells a word.

Operations:

• Insert: O(L) where L = string length
• Search: O(L)
• Prefix search: Find all strings with a given prefix

Applications:

• Autocomplete (type "ca", get "cat", "car")
• Spell-checkers
• IP routing tables (longest prefix match)
• Dictionary implementations

Tries trade space for speed—fast lookups at the cost of memory.

Decision Trees: Machine Learning

In machine learning, decision trees model decisions as branches.

Each internal node tests a feature (e.g., "Age > 30?"). Each branch represents an outcome (yes/no). Leaves assign classifications or predictions.

Example: Predict loan approval

• Root: "Income > $50k?"
  • Yes: "Credit score > 700?" → Approve/Deny
  • No: "Employment > 2 years?" → Approve/Deny

Training: Algorithms like ID3, C4.5, CART recursively split data to maximize information gain or minimize impurity.

Ensemble methods:

• Random forests: Aggregate many decision trees (reduce overfitting)
• Gradient boosting: Train trees sequentially, correcting previous errors

Decision trees are interpretable, handle mixed data types, and don't require feature scaling. They're a cornerstone of ML.

Tree Decompositions: Hard Problems Made Easier

Some NP-hard graph problems become tractable when the graph has tree-like structure.

Tree decomposition: Represent a graph as a tree where each node is a "bag" of vertices. If the graph is "almost a tree" (low treewidth), dynamic programming on the tree decomposition solves problems efficiently.

Applications: Constraint satisfaction, probabilistic inference, circuit analysis.

Real-world networks often have low treewidth, making tree decomposition practically useful.

Catalan Numbers: Counting Binary Trees

How many binary trees with n nodes?

Answer: The nth Catalan number C_n = (1/(n+1)) × C(2n, n).

Examples:

• C_0 = 1 (empty tree)
• C_1 = 1 (single node)
• C_2 = 2 (two shapes)
• C_3 = 5 (five shapes)

Catalan numbers count:

• Binary trees with n nodes
• Ways to parenthesize n+1 factors
• Paths on grid not crossing diagonal
• Balanced parentheses strings

Trees connect to deep combinatorial structures.

Tree Isomorphism: Same Structure, Different Labels

Two trees are isomorphic if there's a relabeling making them identical.

Tree isomorphism is solvable in linear time (unlike general graph isomorphism, which is hard). Algorithm:

1. Compute canonical form (e.g., rooted at centroid, DFS encoding)
2. Compare canonical forms

Why it matters: Matching chemical structures (molecular trees), detecting duplicate data structures, pattern recognition.

Real-World Trees

File Systems

Unix/Linux file systems are trees. Root directory (/) contains subdirectories, which contain files/subdirectories.

Commands like find, ls -R are tree traversals.

XML/HTML

Documents are trees (DOM—Document Object Model). Tags nest hierarchically. Web browsers parse HTML into trees for rendering.

Corporate Org Charts

CEO at root, executives as children, managers below, employees as leaves. Queries: "Who reports to X?" "What's the chain of command?" are tree queries.

Evolutionary Biology

Phylogenetic trees show species relationships. Leaves = current species, internal nodes = common ancestors. Built from genetic data (sequence similarity).

Artificial Neural Networks

Some architectures (e.g., hierarchical models) are trees. Lower layers extract simple features, higher layers combine them hierarchically.

Why Trees Work

Trees eliminate ambiguity. Between any two nodes, there's exactly one path. No cycles means no redundancy. This makes trees:

• Efficient to search: O(log n) for balanced trees
• Easy to understand: Hierarchy is intuitive
• Simple to implement: Recursion matches tree structure naturally
• Space-efficient: n nodes, n-1 edges (minimal connected structure)

Trees are the simplest connected structure. Any more edges and you get cycles (redundancy). Any fewer and you disconnect.

This minimalism makes trees computationally elegant and conceptually clear.

Further Reading

• Cormen, Thomas H., et al. Introduction to Algorithms. MIT Press, 4th edition, 2022. (Chapters on trees, BSTs, heaps)
• Knuth, Donald E. The Art of Computer Programming, Volume 1: Fundamental Algorithms. Addison-Wesley, 3rd edition, 1997. (Trees and data structures)
• Sedgewick, Robert, and Kevin Wayne. Algorithms. Addison-Wesley, 4th edition, 2011. (Tree algorithms and implementations)
• West, Douglas B. Introduction to Graph Theory. Prentice Hall, 2nd edition, 2001. (Trees as graphs)

This is Part 7 of the Discrete Mathematics series, exploring the foundational math of computer science, algorithms, and computational thinking. Next: "Recurrence Relations Explained — Sequences That Define Themselves."

Part 7 of the Discrete Mathematics series.

Previous: Graph Theory: Networks of Nodes and Edges Next: Recurrence Relations: Sequences Defined Recursively