What Is a Logarithm? The Inverse of Exponentiation
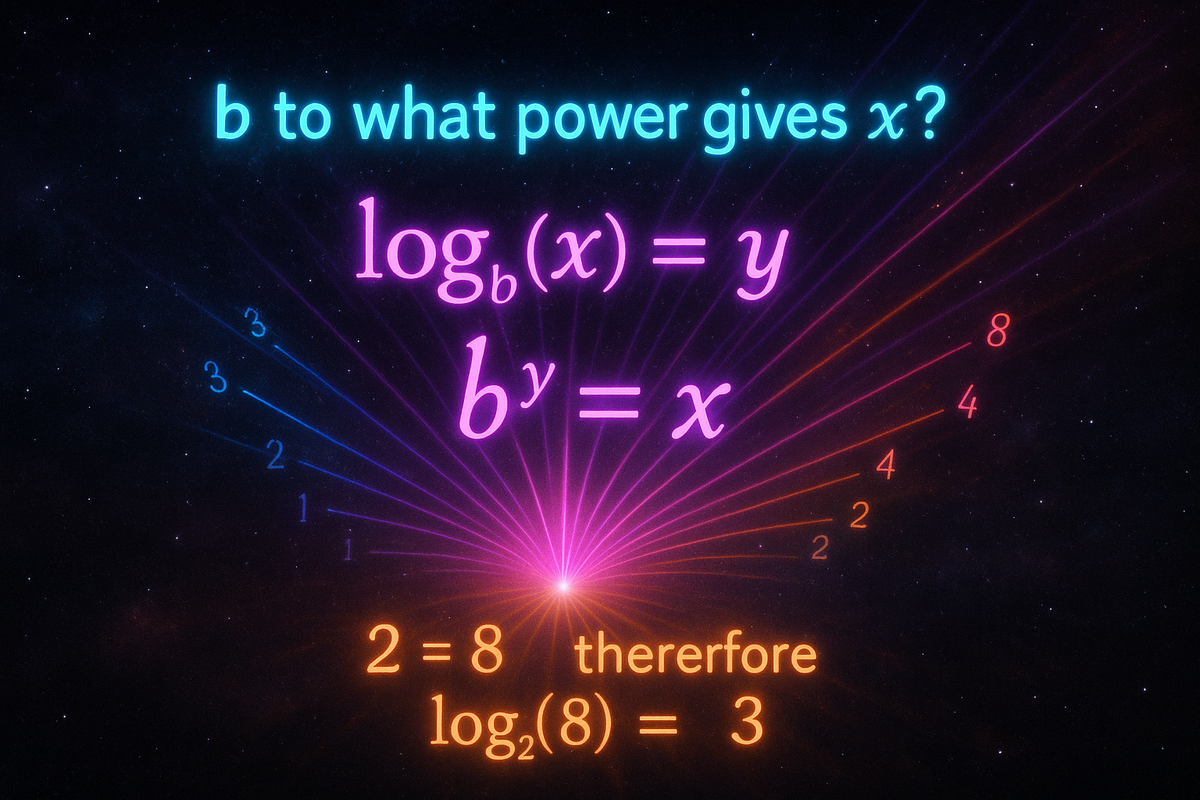
A logarithm answers the question: what exponent gives this result?
2³ = 8. The logarithm asks: what power of 2 produces 8? The answer is 3.
log₂(8) = 3
That's it. A logarithm is an exponent—the exponent you need to raise the base to in order to get the argument.
If exponentiation is the forward operation (base^power = result), then logarithm is the reverse operation (given base and result, find power).
The Definition
log_b(x) = y means bʸ = x
The logarithm base b of x equals y if and only if b to the power y equals x.
These are equivalent statements:
- log₂(8) = 3 ↔ 2³ = 8
- log₁₀(1000) = 3 ↔ 10³ = 1000
- log₃(81) = 4 ↔ 3⁴ = 81
The logarithm extracts the exponent from the exponential equation.
Reading Logarithms
log₁₀(100) = ?
Ask: 10 to what power equals 100?
10² = 100, so log₁₀(100) = 2.
log₂(32) = ?
Ask: 2 to what power equals 32?
2⁵ = 32, so log₂(32) = 5.
log₅(1) = ?
Ask: 5 to what power equals 1?
5⁰ = 1 (any number to the zero power is 1), so log₅(1) = 0.
log₄(1/16) = ?
Ask: 4 to what power equals 1/16?
4⁻² = 1/16, so log₄(1/16) = -2.
Why Logarithms Exist
Logarithms were invented to simplify multiplication.
Before calculators, multiplying large numbers was tedious and error-prone. But logarithms convert multiplication to addition:
log(a × b) = log(a) + log(b)
Instead of multiplying 347 × 829, you could:
- Look up log(347) and log(829) in a table
- Add them
- Look up the antilog to get the answer
This made complex calculations practical. It's why slide rules worked.
Today, calculators handle multiplication. But logarithms remain essential for understanding scales, solving exponential equations, and measuring information.
The Three Common Bases
Common logarithm (base 10): log₁₀(x), often written just log(x)
Used for orders of magnitude, decibels, pH scale.
Natural logarithm (base e): logₑ(x), written ln(x)
Used in calculus, physics, continuous growth. The "natural" base for rates of change.
Binary logarithm (base 2): log₂(x)
Used in computer science, information theory. Measures bits.
Each base has its domain:
- 10 for human-scale counting
- e for continuous mathematics
- 2 for digital information
Key Properties
Property 1: log_b(1) = 0
Because b⁰ = 1 for any base b.
Property 2: log_b(b) = 1
Because b¹ = b.
Property 3: log_b(bˣ) = x
The log "undoes" the exponential. Applying log to b^x gives back x.
Property 4: b^(log_b(x)) = x
The exponential "undoes" the log. Raising b to log_b(x) gives back x.
Properties 3 and 4 say logarithms and exponentials are inverses—like addition/subtraction or multiplication/division.
The Graph
The graph of y = log_b(x) for b > 1:
- Domain: x > 0 (can't take log of zero or negative)
- Range: all real numbers
- Passes through (1, 0) — log of 1 is always 0
- Passes through (b, 1) — log of the base is always 1
- Increases slowly, ever more slowly
- Vertical asymptote at x = 0
The logarithm grows, but grudgingly. It takes exponentially larger inputs to produce linear outputs.
Compare:
- log₁₀(10) = 1
- log₁₀(100) = 2
- log₁₀(1000) = 3
- log₁₀(10,000,000,000) = 10
Ten billion—an enormous number—has a log of only 10.
Logarithms and Inverse Functions
If f(x) = bˣ, then f⁻¹(x) = log_b(x).
Graphically, y = log_b(x) is the reflection of y = bˣ across the line y = x.
Where bˣ shoots up exponentially, log_b(x) rises logarithmically (slowly). Where bˣ has a horizontal asymptote (y = 0), log_b(x) has a vertical asymptote (x = 0).
The two functions are mirror images through the symmetry of inversion.
Solving Exponential Equations
Logarithms are how you solve for x when x is in an exponent.
Example: Solve 2ˣ = 10.
Take log₂ of both sides: x = log₂(10) ≈ 3.32
Or use any base: x = log(10)/log(2) = 1/log(2) ≈ 3.32
Example: Solve 5^(2x-1) = 125.
Note 125 = 5³, so: 5^(2x-1) = 5³ 2x - 1 = 3 x = 2
Example: How long to double at 5% interest?
2 = (1.05)ᵗ log(2) = t × log(1.05) t = log(2)/log(1.05) ≈ 14.2 years
Without logarithms, you couldn't isolate t. The variable is trapped in the exponent.
Domain Restrictions
log_b(x) is only defined for x > 0.
You cannot take the logarithm of zero (what power of b gives 0? None—the answer doesn't exist).
You cannot take the logarithm of a negative number (with real numbers—complex logarithms exist but are different).
These restrictions come from the nature of exponentials: b^y is always positive for b > 0.
Why "Logarithm"?
The word comes from Greek: logos (ratio) + arithmos (number).
Logarithms are the "ratio numbers" that measure how many times you multiply the base to reach the argument.
Napier and Briggs developed logarithms in the early 1600s. For three centuries, log tables were essential tools for scientists, engineers, and navigators.
The slide rule—a mechanical calculator based on logarithms—was standard equipment until electronic calculators appeared in the 1970s.
The Essential Insight
Logarithms reverse exponentiation.
If you understand that 2³ = 8 and log₂(8) = 3 are the same statement from different perspectives, you understand logarithms.
The exponential asks: base^power gives what? The logarithm asks: base^what gives this?
Same relationship. Different unknown. Logarithms find the hidden exponent.
Why Logarithms Matter
- They solve exponential equations. Without logs, you can't isolate x in bˣ = c.
- They compress scales. Vast ranges become manageable numbers.
- They linearize exponentials. Taking logs turns exponential data into linear data.
- They measure information. Bits, entropy, and complexity use logarithms.
- They match human perception. We hear and see logarithmically.
The logarithm is the exponent detector. It reveals the power hidden in exponential relationships.
Part 1 of the Logarithms series.
Previous: Logarithms Explained Next: Log Rules: Why Multiplication Becomes Addition
Comments ()