The Bernoulli Equation: A Clever Substitution

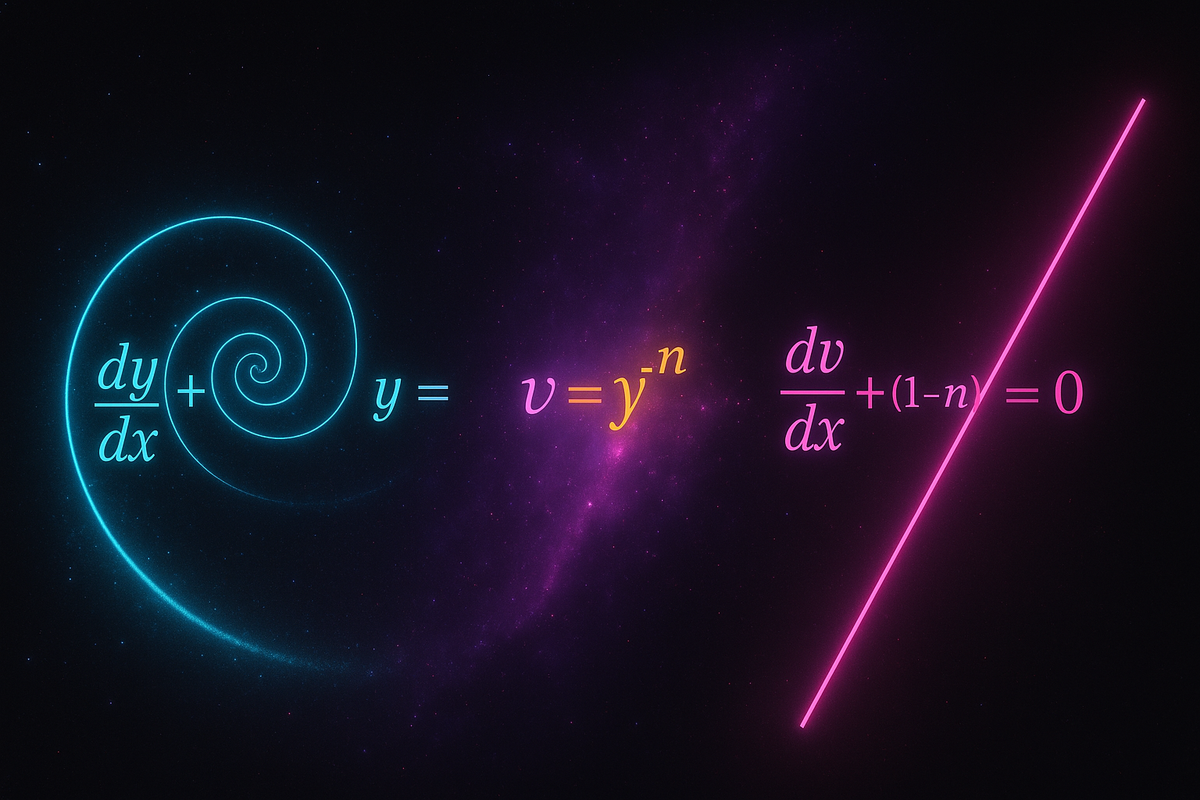
Bernoulli equations are nonlinear but solvable. They look like linear first-order ODEs except for one term—y raised to a power.

Standard form: dy/dx + P(x)y = Q(x)y^n

If n = 0 or n = 1, it's already linear (covered earlier). But for n ≠ 0, 1, the y^n term makes it nonlinear.

The trick: a clever substitution transforms it into a linear equation, which you already know how to solve.

It's a beautiful example of mathematical judo—convert a hard problem into an easy one by changing variables.

What Makes It a Bernoulli Equation

Standard form: dy/dx + P(x)y = Q(x)y^n

Key features:

• First-order
• y and dy/dx appear linearly on the left
• y^n (nonlinear term) appears on the right

Examples:

dy/dx + y = y² (n = 2)

dy/dx - (2/x)y = x²y³ (n = 3)

dy/dx + y/x = xy^(-1) (n = -1)

All Bernoulli equations. The exponent n distinguishes them from linear.

Why It's Nonlinear

The term y^n (for n ≠ 0, 1) makes the equation nonlinear.

If n = 2: dy/dx + P(x)y = Q(x)y²

This is quadratic in y. Superposition fails—if y₁ and y₂ are solutions, y₁ + y₂ generally isn't.

Nonlinearity means no systematic general method exists. But for this specific structure (Bernoulli form), substitution works.

The Substitution

The key: Let v = y^(1-n).

Then: dv/dx = (1-n)y^(-n)(dy/dx)

Rearrange: dy/dx = (1/(1-n))y^n(dv/dx)

Substitute into the Bernoulli equation.

Original: dy/dx + P(x)y = Q(x)y^n

Replace dy/dx:

(1/(1-n))y^n(dv/dx) + P(x)y = Q(x)y^n

Divide through by y^n:

(1/(1-n))(dv/dx) + P(x)y^(1-n) = Q(x)

But v = y^(1-n), so:

(1/(1-n))(dv/dx) + P(x)v = Q(x)

Multiply by (1-n):

dv/dx + (1-n)P(x)v = (1-n)Q(x)

This is linear in v. Solve using the integrating factor method, then back-substitute v = y^(1-n) to get y.

Example 1: Bernoulli with n = 2

Solve: dy/dx + y = y²

Here P(x) = 1, Q(x) = 1, n = 2.

Step 1: Substitute v = y^(1-2) = y^(-1).

Then: dv/dx = -y^(-2)(dy/dx), so dy/dx = -y²(dv/dx).

Step 2: Substitute into equation:

-y²(dv/dx) + y = y²

Divide by y²:

-(dv/dx) + y^(-1) = 1

But v = y^(-1):

-(dv/dx) + v = 1

Multiply by -1:

dv/dx - v = -1

Step 3: This is linear in v. Standard form: dv/dx - v = -1.

Integrating factor: μ = e^(-∫1 dx) = e^(-x).

Multiply: e^(-x)(dv/dx) - e^(-x)v = -e^(-x)

Left side is d/dx[e^(-x)v]:

d/dx[e^(-x)v] = -e^(-x)

Integrate: e^(-x)v = ∫-e^(-x)dx = e^(-x) + C

v = 1 + Ce^x

Step 4: Back-substitute v = 1/y:

1/y = 1 + Ce^x

y = 1/(1 + Ce^x)

General solution: y = 1/(1 + Ce^x)

Check: Differentiate and verify it satisfies the original equation. (It does.)

Example 2: Bernoulli with n = 3

Solve: dy/dx - (2/x)y = x²y³

Here P(x) = -2/x, Q(x) = x², n = 3.

Step 1: Substitute v = y^(1-3) = y^(-2).

Then: dv/dx = -2y^(-3)(dy/dx), so dy/dx = -(1/2)y³(dv/dx).

Step 2: Substitute into equation:

-(1/2)y³(dv/dx) - (2/x)y = x²y³

Divide by y³:

-(1/2)(dv/dx) - (2/x)y^(-2) = x²

But v = y^(-2):

-(1/2)(dv/dx) - (2/x)v = x²

Multiply by -2:

dv/dx + (4/x)v = -2x²

Step 3: This is linear in v.

Integrating factor: μ = e^(∫(4/x)dx) = e^(4ln|x|) = x⁴.

Multiply: x⁴(dv/dx) + 4x³v = -2x⁶

Left side is d/dx[x⁴v]:

d/dx[x⁴v] = -2x⁶

Integrate: x⁴v = ∫-2x⁶dx = -(2/7)x⁷ + C

v = -(2/7)x³ + Cx^(-4)

Step 4: Back-substitute v = 1/y²:

1/y² = -(2/7)x³ + Cx^(-4)

y² = 1/(-(2/7)x³ + Cx^(-4)) = x⁴/(Cx⁴ - (2/7)x⁷) = x⁴/(C - (2/7)x³)

y = ±√(x⁴/(C - (2/7)x³))

Messy, but valid. The point: substitution converted nonlinear to linear.

Example 3: Negative Exponent

Solve: dy/dx + y/x = xy^(-1)

Here n = -1, P(x) = 1/x, Q(x) = x.

Step 1: Substitute v = y^(1-(-1)) = y².

Then: dv/dx = 2y(dy/dx), so dy/dx = (1/(2y))(dv/dx).

Step 2: Substitute:

(1/(2y))(dv/dx) + y/x = xy^(-1)

Multiply by 2y:

dv/dx + (2y²)/x = 2x

But v = y²:

dv/dx + (2v)/x = 2x

Step 3: Linear in v.

Integrating factor: μ = e^(∫(2/x)dx) = e^(2ln|x|) = x².

Multiply: x²(dv/dx) + 2xv = 2x³

Left side is d/dx[x²v]:

d/dx[x²v] = 2x³

Integrate: x²v = ∫2x³dx = (1/2)x⁴ + C

v = (1/2)x² + Cx^(-2)

Step 4: Back-substitute v = y²:

y² = (1/2)x² + Cx^(-2)

y = ±√((1/2)x² + C/x²)

General solution (implicit form acceptable).

When to Use Bernoulli Substitution

Use when:

• Equation has form dy/dx + P(x)y = Q(x)y^n
• n ≠ 0 and n ≠ 1 (otherwise it's already linear or separable)

The substitution v = y^(1-n) always linearizes.

Why This Works

The Bernoulli equation mixes linear and nonlinear terms in a specific way. The nonlinearity is isolated in the y^n term.

The substitution v = y^(1-n) "undoes" that nonlinearity. When you differentiate v, you pull down a factor of y^(-n) from the chain rule, which cancels the y^n in the original equation.

It's engineered to work. The form of the substitution is tailored to the structure of the equation.

Connection to Logistic Equation

The logistic equation dy/dx = ry(1 - y/K) can be written as:

dy/dx = ry - (r/K)y²

Rearrange: dy/dx - ry = -(r/K)y²

This is Bernoulli with P(x) = -r, Q(x) = -r/K, n = 2.

Apply substitution v = y^(-1):

dv/dx + rv = r/K

Linear. Solve:

Integrating factor: μ = e^(rt)

d/dx[e^(rt)v] = (r/K)e^(rt)

e^(rt)v = (1/K)e^(rt) + C

v = 1/K + Ce^(-rt)

Back-substitute v = 1/y:

1/y = 1/K + Ce^(-rt)

y = K/(1 + CKe^(-rt))

This is the standard logistic solution. Bernoulli substitution provides an alternative derivation to separation of variables.

Riccati Equations (Generalization)

A further generalization: Riccati equation.

dy/dx = P(x) + Q(x)y + R(x)y²

This is quadratic in y (like Bernoulli with n = 2) but with an additional P(x) term.

Riccati equations generally can't be solved in closed form unless you know one particular solution. If you have y₁ (a particular solution), you can reduce it to Bernoulli via substitution y = y₁ + 1/v.

Bernoulli is a special case of Riccati where P(x) = 0.

Practical Tips

Tip 1: Always check if n = 0 or n = 1 first. If so, use simpler methods (linear or separable).

Tip 2: The substitution v = y^(1-n) is standard. Memorize it.

Tip 3: After substitution, you get a linear equation in v. Use integrating factor.

Tip 4: Don't forget to back-substitute at the end to recover y.

Tip 5: Solutions can be implicit or messy. That's okay—differential equations don't always yield neat formulas.

When Bernoulli Appears

Bernoulli equations model systems where growth/decay rate depends on a power of the current state.

Population with limited resources: dP/dt = rP - aP² (Bernoulli with n = 2)

Chemical reactions: dC/dt = k₁C - k₂C² (autocatalytic reactions)

Spread of information: dI/dt = αI - βI² (logistic-like models)

Anytime you have linear term ± nonlinear power term, consider Bernoulli.

Summary of Method

To solve dy/dx + P(x)y = Q(x)y^n:

1. Check if n = 0 or 1 (if so, use simpler methods)
2. Substitute v = y^(1-n)
3. Differentiate: dv/dx = (1-n)y^(-n)(dy/dx)
4. Replace dy/dx and simplify to get linear equation in v
5. Solve linear equation using integrating factor
6. Back-substitute v = y^(1-n) to find y

It's algorithmic once you recognize the form.

Next: systems of differential equations, where multiple variables evolve together.

Part 9 of the Differential Equations series.

Previous: Euler's Method: Numerical Approximation Step by Step Next: Systems of ODEs: When Multiple Quantities Change Together