Differential Equations Explained

Holy shit, differential equations are everywhere.
Every time something changes—temperature cooling, populations growing, planets orbiting—differential equations describe it. They're not abstract mathematical curiosities. They're the language reality speaks when it moves.
A differential equation is an equation involving rates of change. Instead of asking "what is x?" you ask "how fast is x changing?" That shift—from states to rates—unlocks modeling anything dynamic.
This series breaks down everything you need to understand differential equations, from foundational concepts to solution techniques to real-world applications.
What You'll Learn
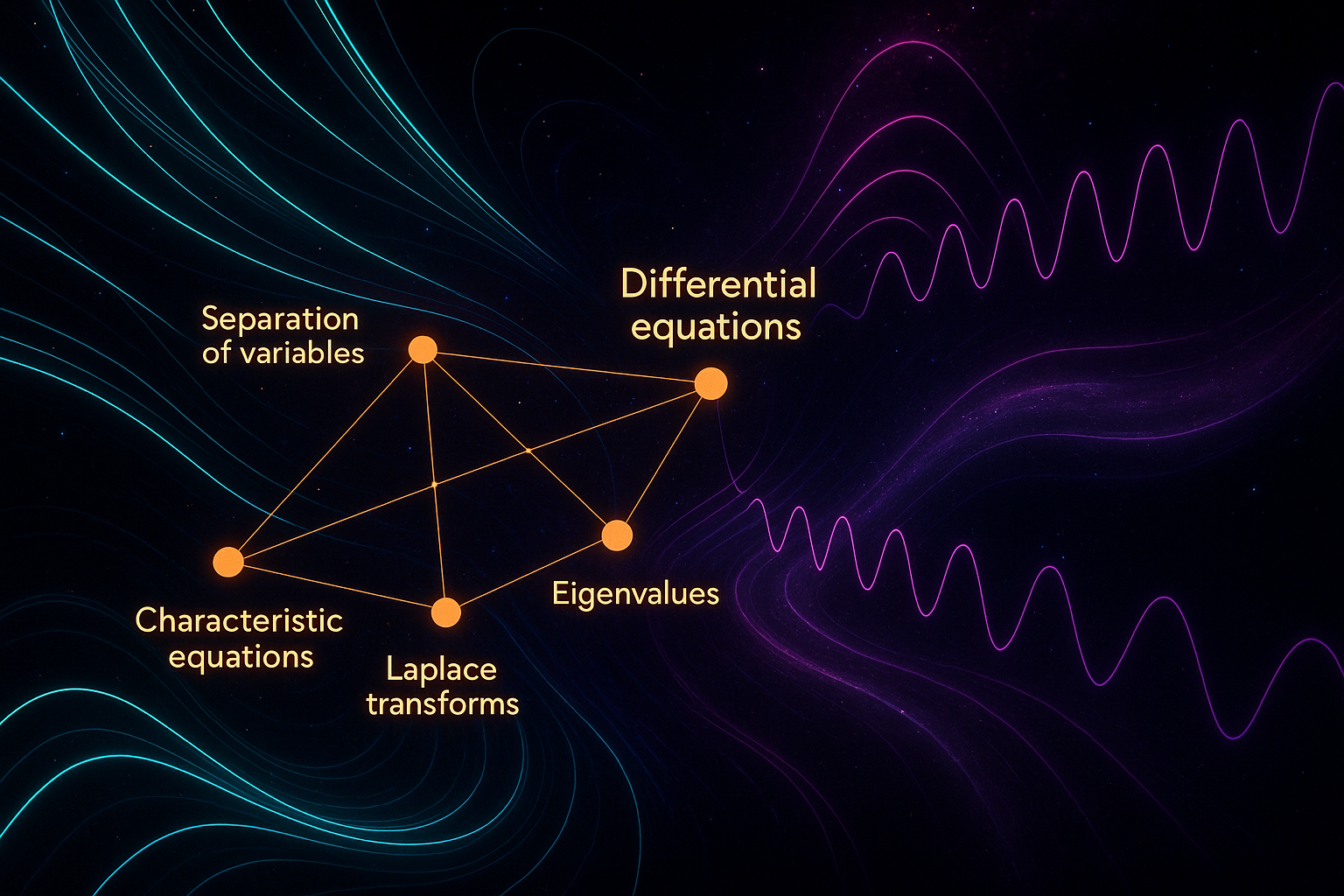
Foundations: Start with what differential equations actually are and the crucial distinction between ordinary and partial differential equations.
First-Order Techniques: Master first-order ODEs, then dive into specific solution methods: separable equations and linear first-order equations.
Second-Order Methods: Graduate to second-order linear ODEs and the powerful characteristic equation technique.
Numerical Approaches: When analytical solutions fail, Euler's method gives you numerical approximations that actually work.
Advanced Techniques: Tackle Bernoulli equations, systems of differential equations, and the transform-based sorcery of Laplace transforms.
Synthesis: Finally, see how it all connects and why differential equations matter for understanding physical reality.
Why This Matters
Differential equations aren't just about solving textbook problems. They're about modeling change itself—the mathematics of becoming rather than being.
Every field that deals with dynamic systems uses differential equations: physics, biology, economics, engineering, neuroscience. If you want to understand how things actually work—not just their static properties but their evolution over time—you need differential equations.
Let's start with the basics: what is a differential equation?
This is the hub page for the Differential Equations series.
Next: What Is a Differential Equation? When Change Depends on the Current State
The Series


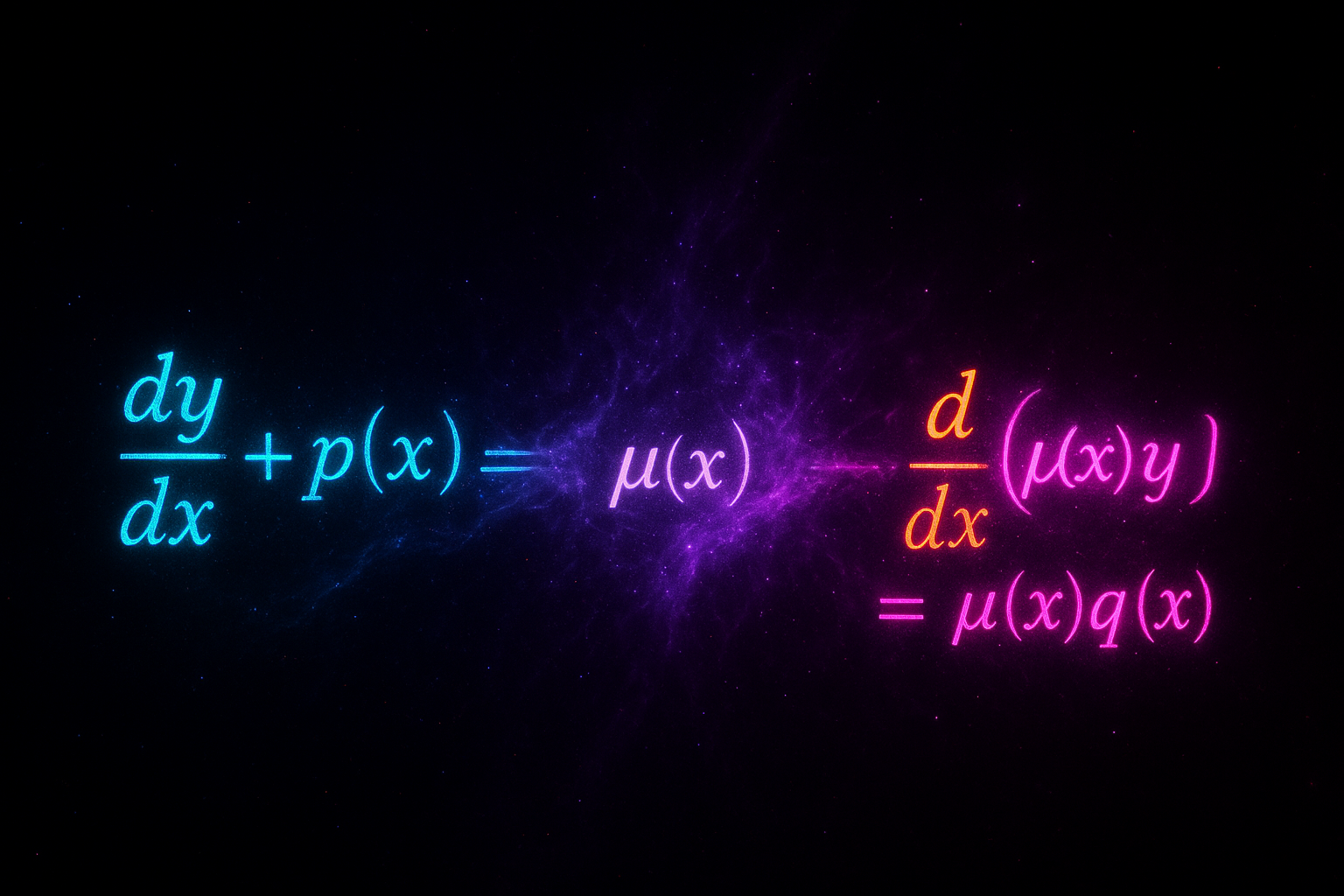

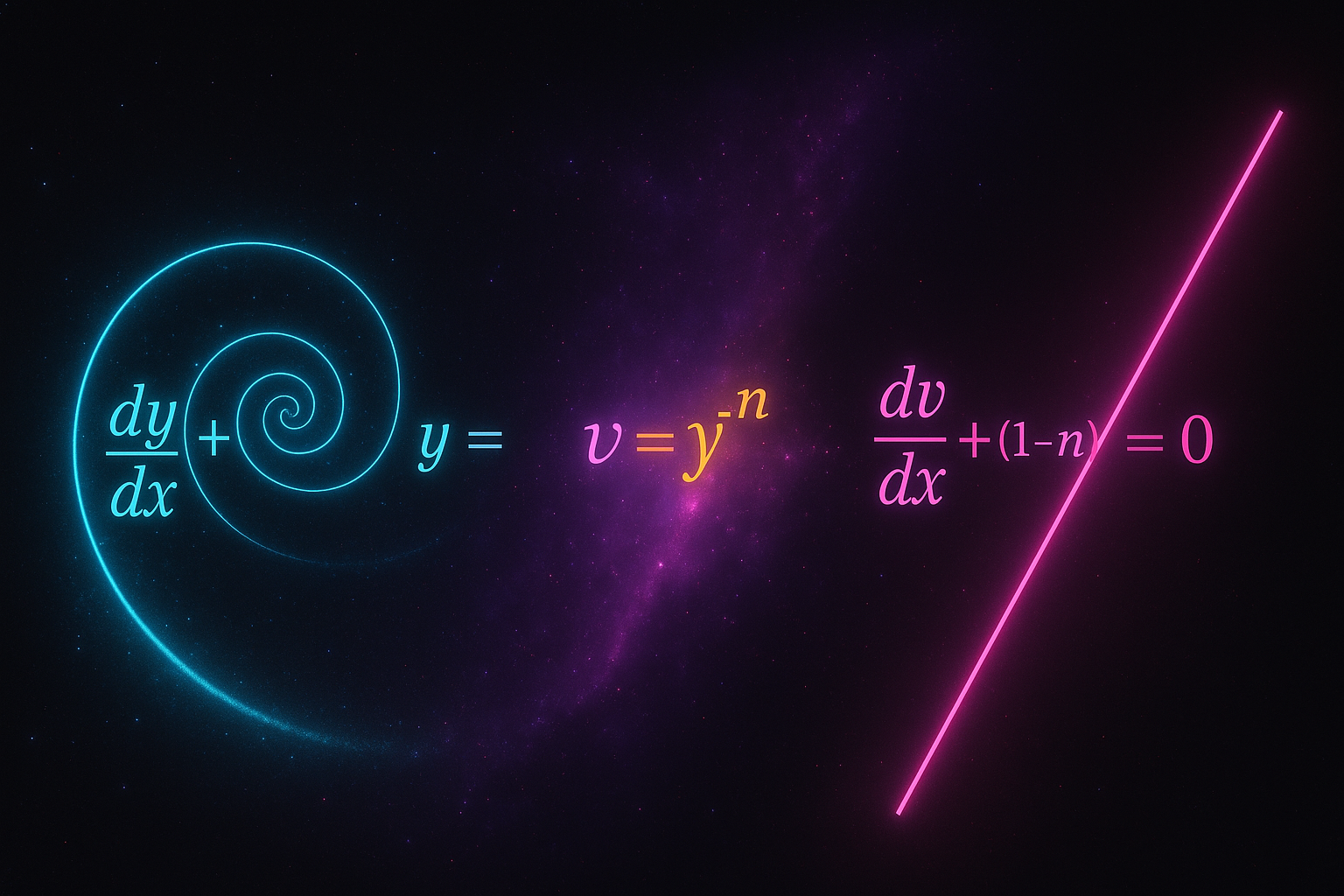

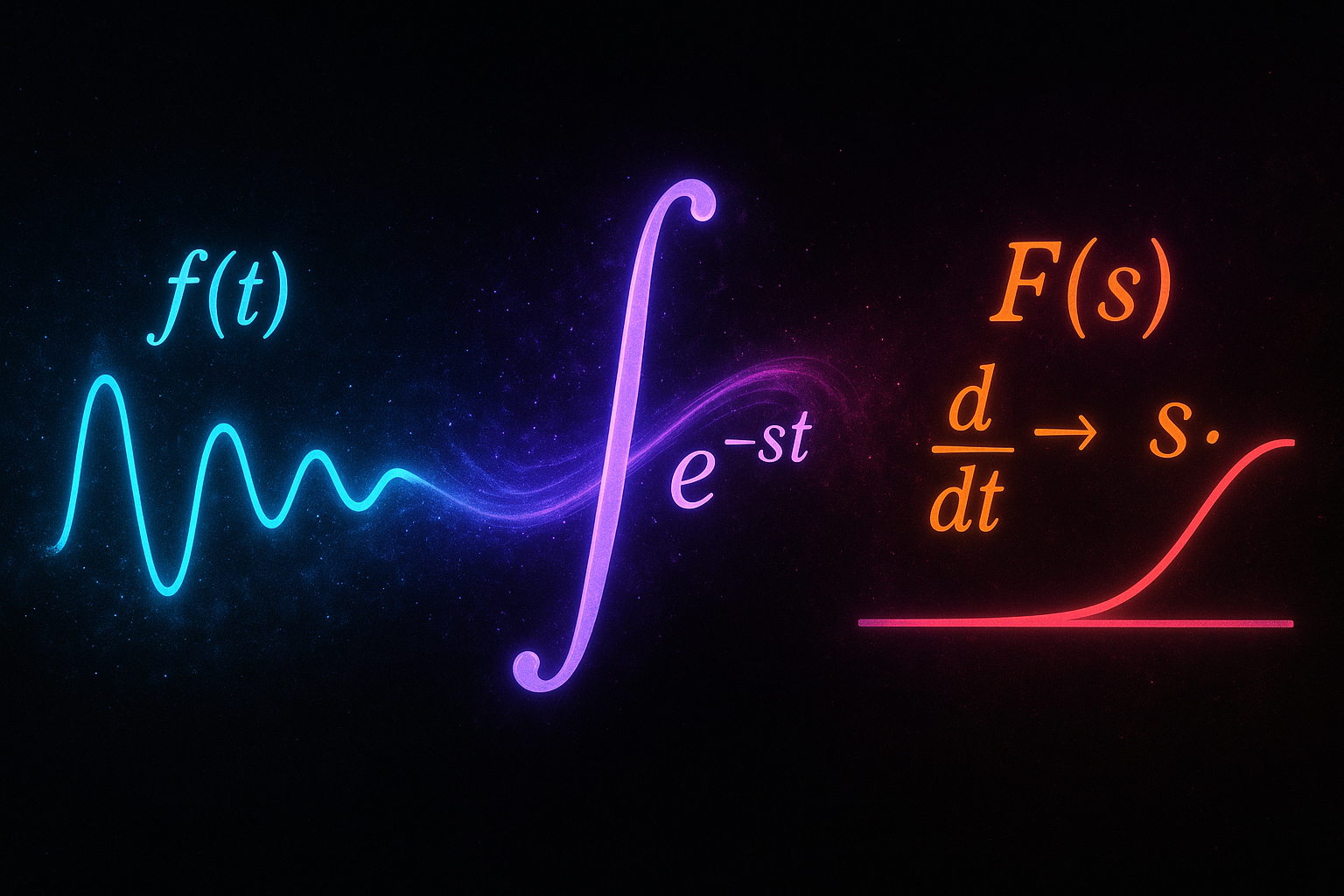
Comments ()