Multivariable Calculus Explained

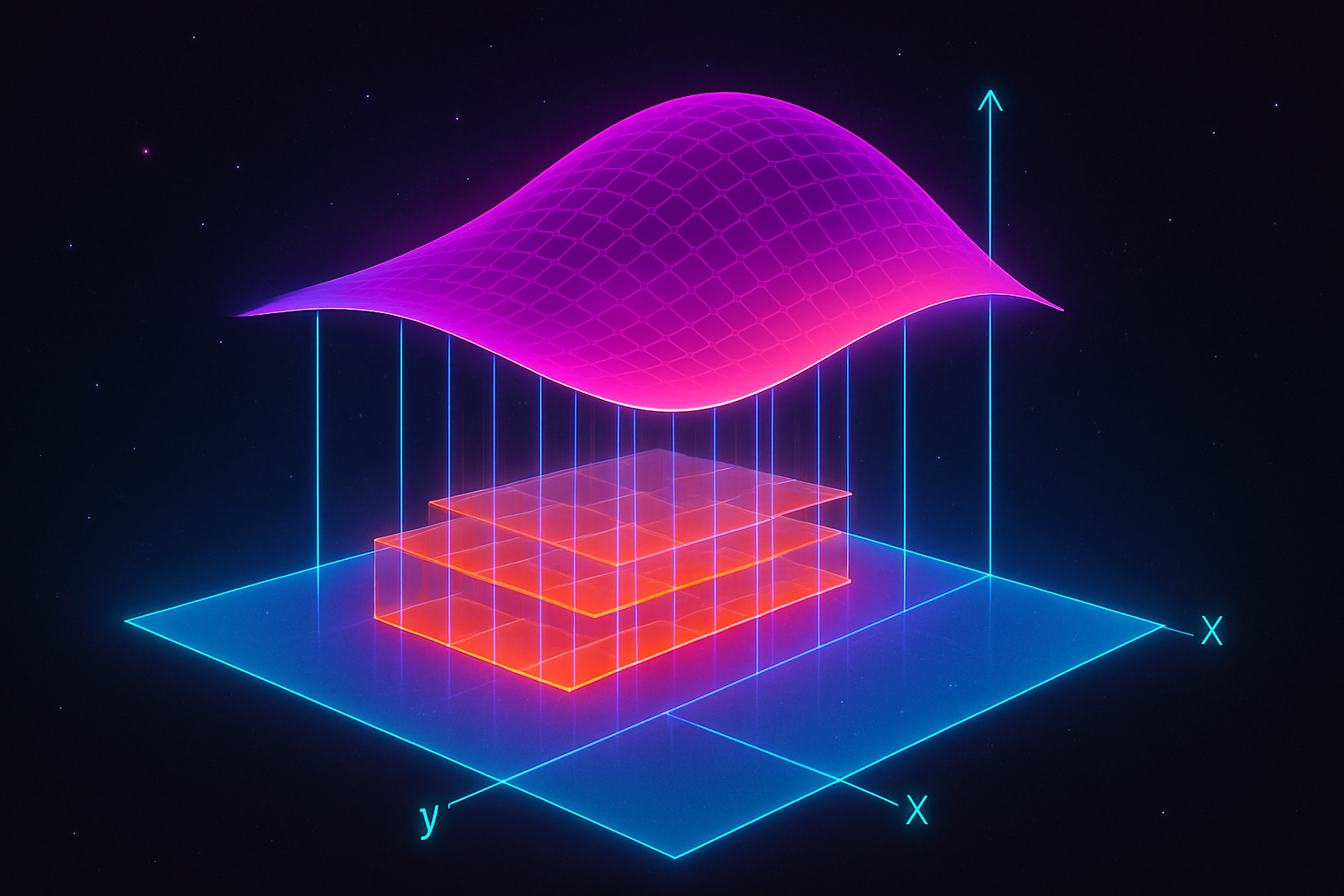
Single-variable calculus taught you how to analyze motion along a line. Multivariable calculus? That's where you break free into actual space—surfaces, volumes, fields that swirl in three dimensions or more.

This is the mathematics of reality as it actually exists: functions that depend on multiple inputs simultaneously, changes that ripple through interconnected systems, optimization problems where everything constrains everything else.

Here's what makes multivariable calculus extraordinary: it's not just "calculus but harder." It's a fundamentally different way of thinking about change, flow, and accumulation when you can't reduce the world to a single axis.

The Series Map

Foundation Concepts:

• What Is Multivariable Calculus - The jump from lines to spaces
• Partial Derivatives Explained - Isolating change in one direction
• The Gradient Explained - Vectors that point uphill

Differentiation Techniques:

• Directional Derivatives - Change along any path you choose
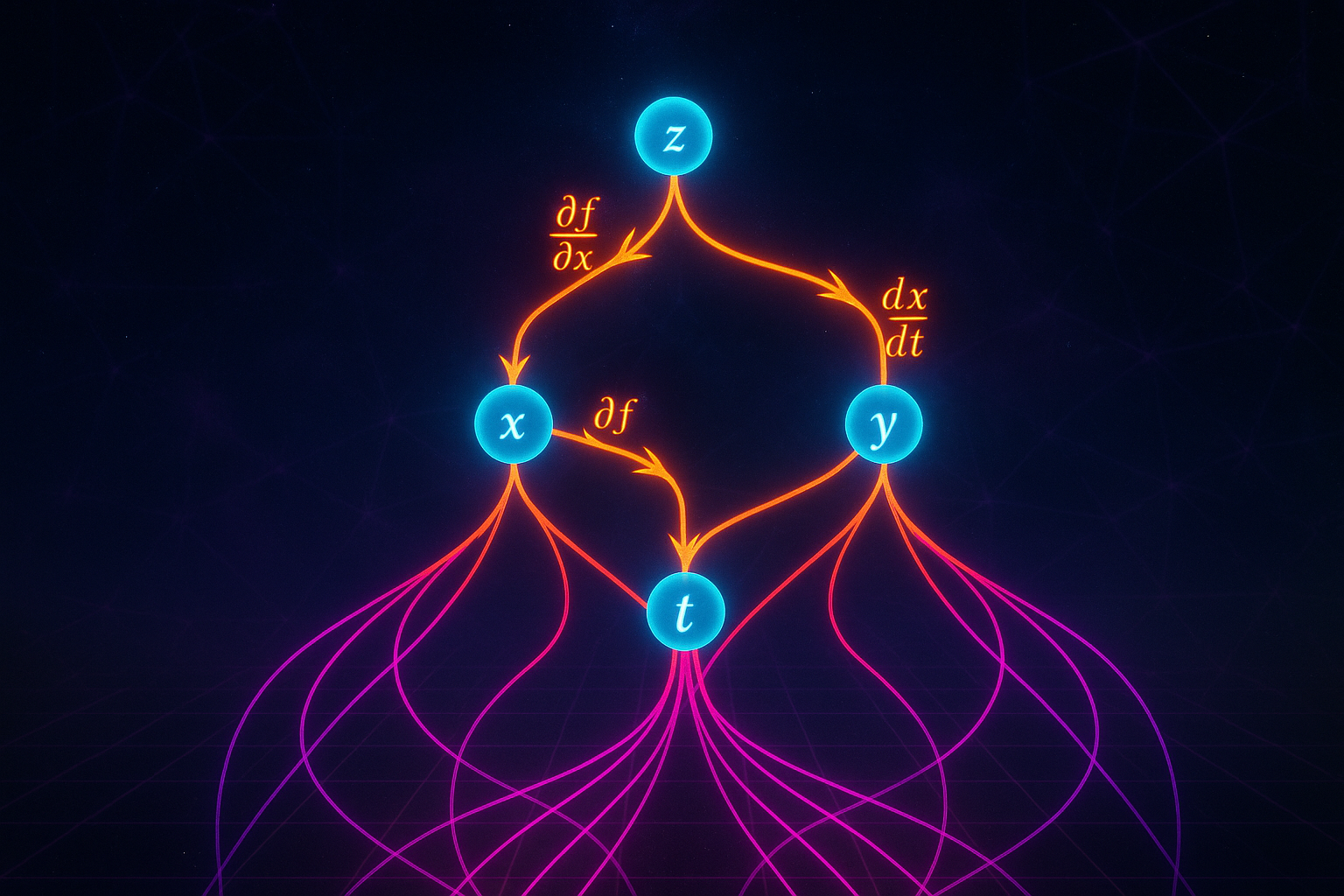
• Multivariable Chain Rule - Tracking dependencies through networks

Integration Methods:

• Double Integrals Explained - Accumulating over regions
• Triple Integrals Explained - Volumes and densities in 3D
• Jacobians and Change of Variables - Warping coordinate systems

Optimization:

• Lagrange Multipliers Explained - Finding extrema under constraints

Synthesis:

• Multivariable Calculus Synthesis - How it all connects

Why This Matters

Temperature doesn't just vary along a thermometer—it forms fields across space. Fluid doesn't flow in one dimension—it swirls in three. Optimization problems in the real world never have just one variable to tune.

Multivariable calculus is the language for describing systems where everything depends on everything else, where change propagates through multiple dimensions simultaneously, where the geometry of the problem shapes the calculus you need.

This is mathematics not as abstraction but as direct engagement with how the world actually works when you stop pretending it's one-dimensional.

This is the hub page for the Multivariable Calculus series.

Next: What Is Multivariable Calculus? When Functions Have Multiple Inputs

The Series

What Is Multivariable Calculus? When Functions Have Multiple Inputs

Multivariable calculus extends derivatives and integrals to functions of several variables

Ideasthesia

Partial Derivatives: Rates of Change in One Direction

Partial derivatives hold all but one variable constant - how does f change with x alone

Ideasthesia

The Gradient: All Partial Derivatives in One Vector

The gradient is a vector of partial derivatives - points in the direction of steepest increase

Ideasthesia

Directional Derivatives: Rates of Change in Any Direction

Directional derivatives measure change along any vector - the gradient projects onto the direction

Ideasthesia

The Chain Rule in Multiple Variables

The multivariable chain rule tracks dependencies - partial derivatives compose through paths

Ideasthesia

Double Integrals: Integrating Over Regions

Double integrals compute volumes under surfaces - integrate twice over a region

Ideasthesia

Triple Integrals: Integrating Through Volumes

Triple integrals sum quantities throughout volumes - mass center of mass moments

Ideasthesia

Change of Variables: Jacobians and Coordinate Transforms

Change of variables transforms integrals - the Jacobian accounts for stretching

Ideasthesia

Lagrange Multipliers: Optimization Under Constraints

Lagrange multipliers find extrema when constraints must be satisfied

Ideasthesia

Synthesis: Multivariable Calculus as the Language of Fields

Multivariable calculus describes how quantities vary across space

Ideasthesia