Vector Calculus Explained

Vector calculus is calculus that works with things that have direction. It's the mathematics of flow, force, and fields—the language you need to describe anything that moves through space.
Regular calculus taught you about functions like f(x) = x². Vector calculus extends that machinery to vector fields: functions that assign a vector (magnitude and direction) to every point in space. Think wind patterns, electromagnetic fields, fluid flow. Anywhere you have "something happening everywhere," you need vector calculus.
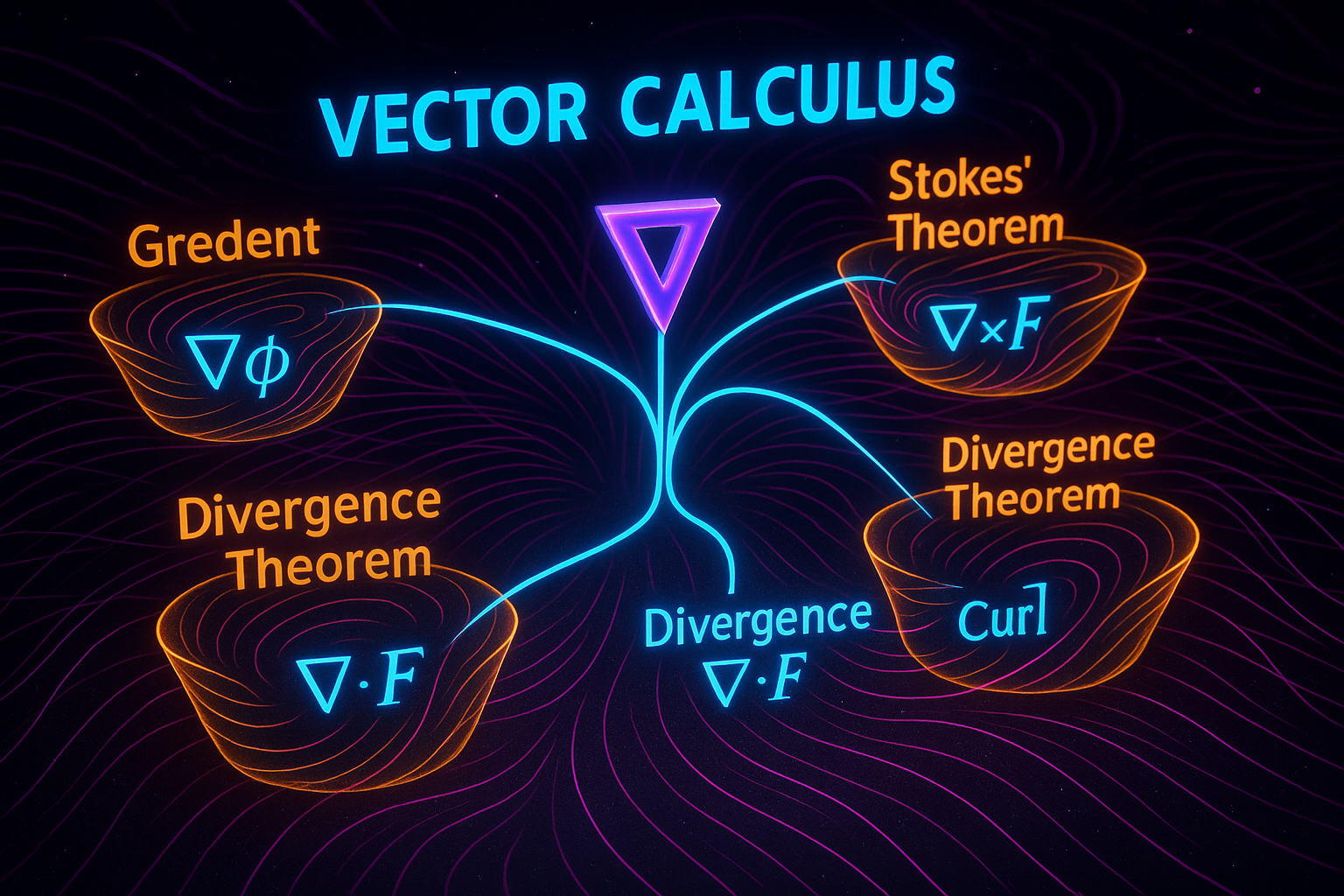
The field divides into three core areas:
Vector fields and their properties. These are functions that map points to vectors. Understanding how to visualize them and what they represent is the foundation everything else builds on.
Integration along paths and surfaces. Line integrals let you calculate work done along curves. Surface integrals let you calculate flux through surfaces. These extend the basic integral to structured paths through space.
Differential operators and the fundamental theorems. Divergence measures spreading. Curl measures rotation. The del operator unifies these concepts. And the three great theorems—Green's, Stokes', and the Divergence Theorem—connect local properties to global behavior, just like the fundamental theorem of calculus connects derivatives to integrals.
This series walks through the entire structure:
- What is Vector Calculus? - The big picture and why it matters
- Vector Fields Explained - Functions that assign vectors to space
- Line Integrals Explained - Integration along curves
- Surface Integrals Explained - Integration over surfaces
- Divergence Explained - Sources and sinks in fields
- Curl Explained - Rotation in vector fields
- The Del Operator Explained - The master differential operator
- Green's Theorem Explained - The 2D fundamental theorem
- Stokes' Theorem Explained - Generalizing to 3D surfaces
- The Divergence Theorem Explained - Gauss's theorem
- Maxwell's Equations via Vector Calculus - Electromagnetism unified
- Vector Calculus Synthesis - How it all connects
Each piece builds on what came before. Start with vector fields, understand the operators, then see how the theorems tie everything into one unified framework. By the end, you'll understand why Maxwell's equations look the way they do—and why vector calculus is the natural language for describing physical reality.
This is the hub page for the Vector Calculus series.
Next: What Is Vector Calculus? The Mathematics of Fields
The Series










Comments ()